WHY?

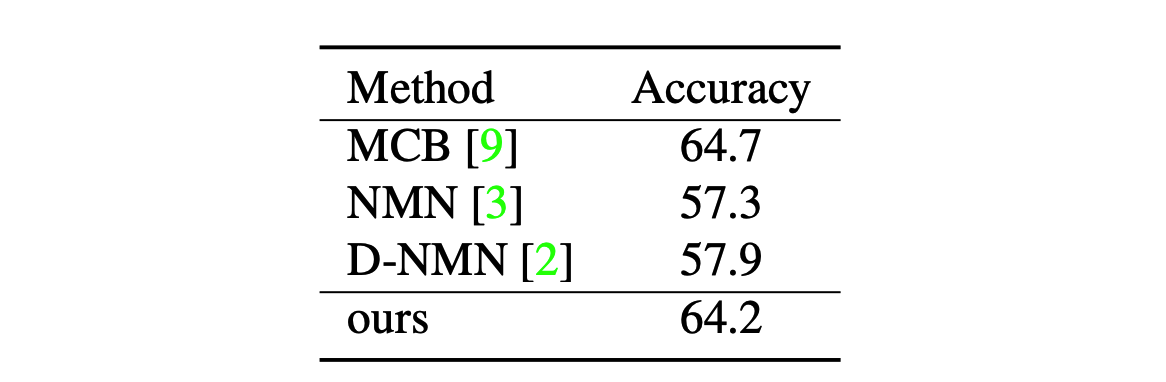
Former neural module network for VQA depends on a naive semantic parser to unroll the layout of the network. This paper suggests End-to-End Module Networks(N2NMN) to directly learn the layout from the data.

WHAT?

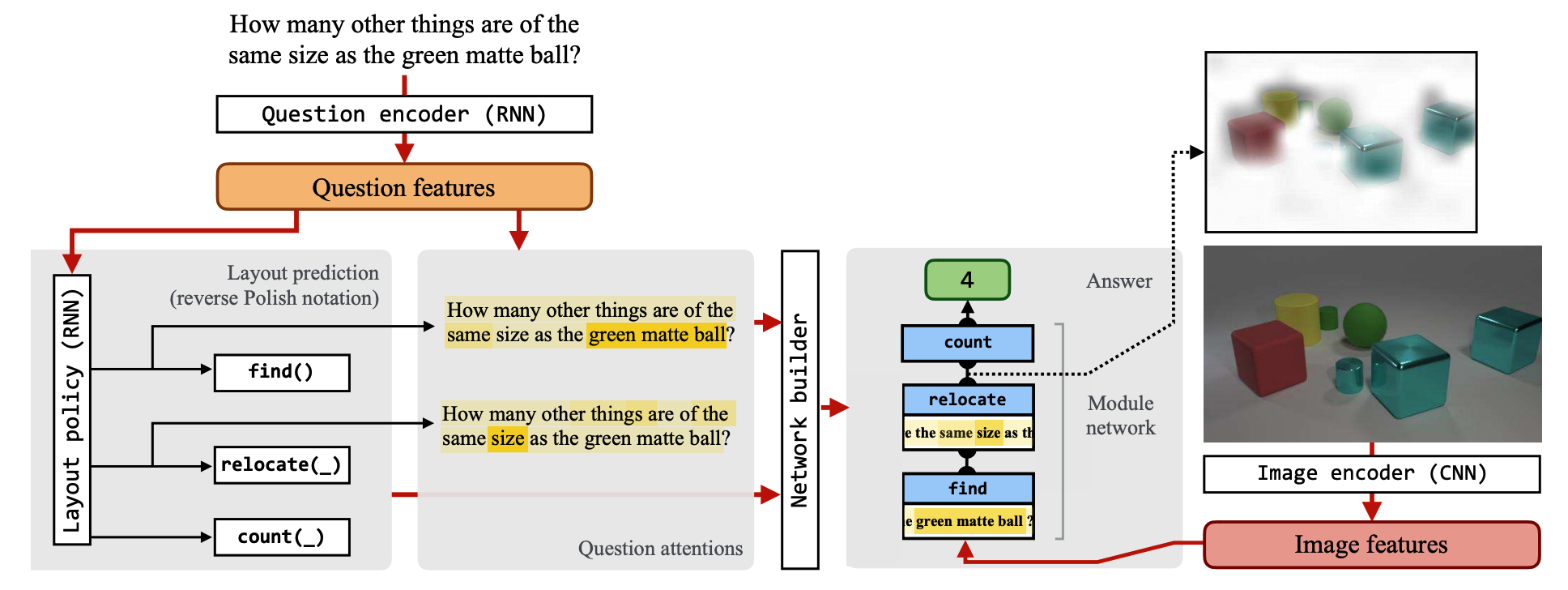
Layout policy select one of the predefined modules.

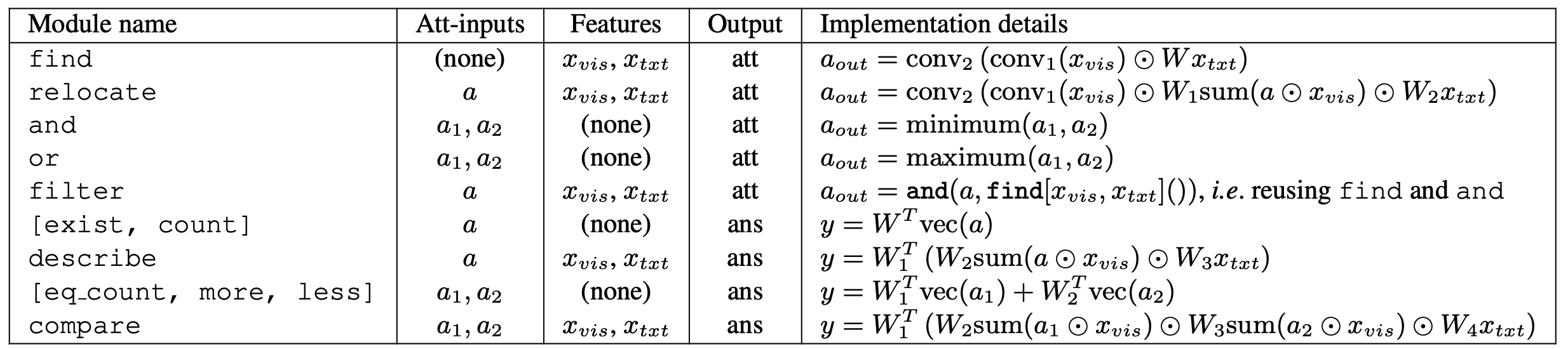
Instead of using semantic parser to get the layout for the modules from question, N2NMN use encoder-decoder structure to train them. RNN is used for question encoder and another RNN(with attention) is used for layout policy. Beam search is used to get the layout of the maximum probability.

$$u_{ti} = v^{\top}tanh(W_1 h_i + W_2 h_t)\\ \alpha_{ti} = \frac{exp(u_{ti})}{\sum_{j=1}^T exp(u_{tj})}\\ c_t = \sum_{i=1}^T \alpha_{ti} h_i\\ p(m^{(t)}|m^{(1)},...,m^{(t-1)}, q) = softmax(W_3 h_t + W_4 c_t)$$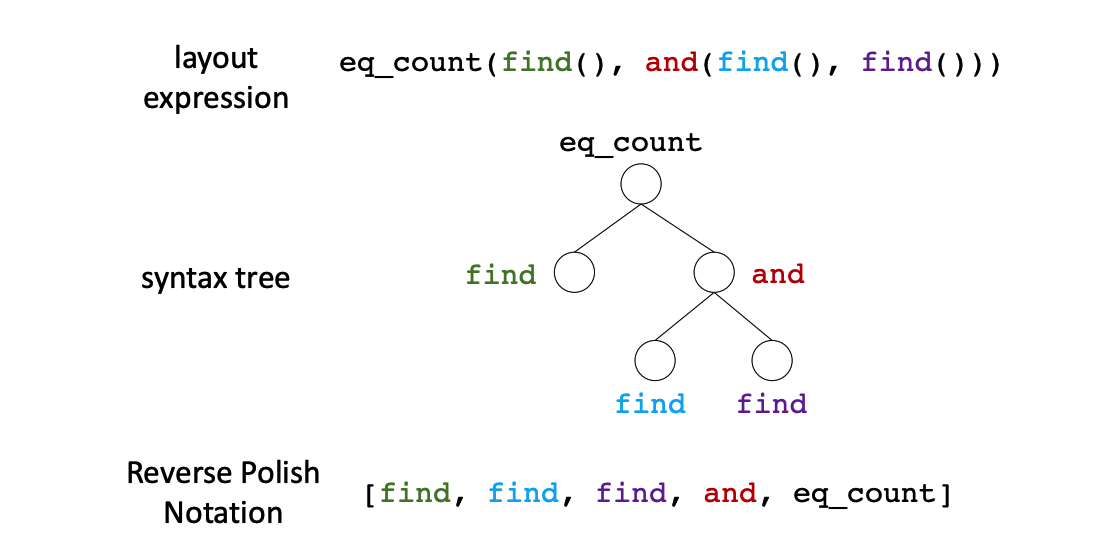

The sequence of modules from decoder is mapped into a syntax tree using Reverse Polish Notation(the post-order traversal). Since the layout policy is not fully differentiable, REINFORCE algorithm is used to approximate the gradient. Entropy regularization(0.005) is used to encourage exploration.

$$L(\theta) = E_{l\sim p(l|q;\theta)}[\tilde{L}(\theta, l; q, I)]\\ \nabla L \approx \frac{1}{M}\sum_{m=1}^M ([\tilde{L}(\theta, l_m) - b]\nabla_{\theta}log p(l_m|q;\theta) + \nabla_{\theta}\tilde{L}(\theta, l_m))$$

Since learning the layout from the scratch is challenging, additional knowledge(expert policy) can be provided for initialization. KL-divergence between layout policy and expert policy is added to loss function.

So?

N2NMN showed better result than NMN on SHAPES, CLEVR and VQA. The expert policies of SHAPES and CLEVER are provided in the dataset, and stanford parser is used for VQA.

The layout policy is shown to learn the appropriate policy. Learning from expert policy is shown to be even better than cloning the expert policy.

Hu, Ronghang, et al. “Learning to reason: End-to-end module networks for visual question answering.” CoRR, abs/1704.05526 3 (2017).