WHY?

While bilinear model is an effective method for capturing the relationship between two spaces, often the number of parameters is intractable. This paper suggests to reduce the number of parameters by controlling the rank of the matrix with Turker decomposition.

Note

With $\times_i$ denotes the i-mode product between a tensor and a matrix, Tucker decomposition of a tensor $\tau$ is as follows.

$$\mathbf{\tau} \in \mathbb{R}^{d_q \times d_v \times |\mathcal{A}|}\\ \mathbf{\tau} = ((\mathbf{\tau_c} \times_1 \mathbf{W}_q) \times_2 \mathbf{W}_v) \times_3 \mathbf{W}_O$$

WHAT?

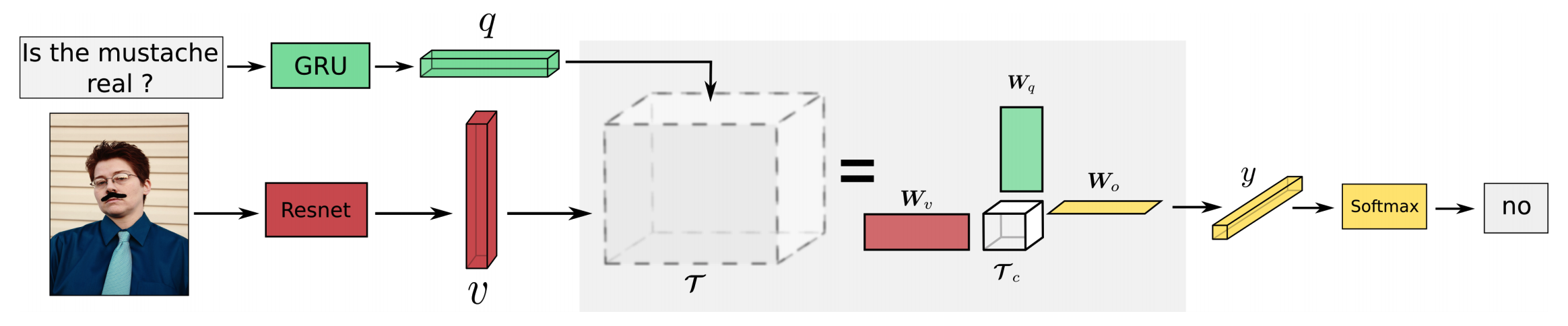
The Tucker decomposition showed that a tensor can be represented with a limited number of parameters. The bilinear relationship between question vectors and image vectors can be represented in a Tucker Fusion form.

$$\mathbf{\tau} = ((\mathbf{\tau_c} \times_1 (\mathbf{q}^{\top}\mathbf{W}_q)) \times_2 (\mathbf{v}^{\top}\mathbf{W}_v)) \times_3 \mathbf{W}_O\\ \mathbf{z} = (\mathbf{\tau}_c \times_1 \mathbf{\tilde{q}}) \times_2 \mathbf{\tilde{v}} \in \mathbb{R}^{t_o}\\ \mathbf{y} = \mathbf{z}^{\top}\mathbf{W}_O$$

We can control the sparsity and expressiveness of bilinear model by controlling the rank of a slice of $\mathbf{\tau}_c$. If we impose the rank of a slice of the core matrix to be R, then each slice can be represented with the sum of R rank one matrices.

$$\mathbf{z}[k] = \tilde{\mathbf{q}}^{\top}\mathbf{\tau}_c[:,:,k]\tilde{\mathbf{v}}\\ \mathbf{\tau}_c[:,:,k] = \sum_{r=1}^R \mathbf{m}_r^k \otimes \mathbf{n}_r^{k\top}\\ \mathbf{z}[k] = \sum_{r=1}^R(\tilde{\mathbf{q}}^{\top}\mathbf{m}_r^k)(\tilde{\mathbf{v}}^{\top}\mathbf{n}_r^k)\\ \mathbf{z} = \sum_{r=1}^R \mathbf{z}_r\\ \mathbf{z}_r = (\tilde{\mathbf{q}}^{\top}\mathbf{M}_r)*(\tilde{\mathbf{v}}^{\top}\mathbf{N}_r)$$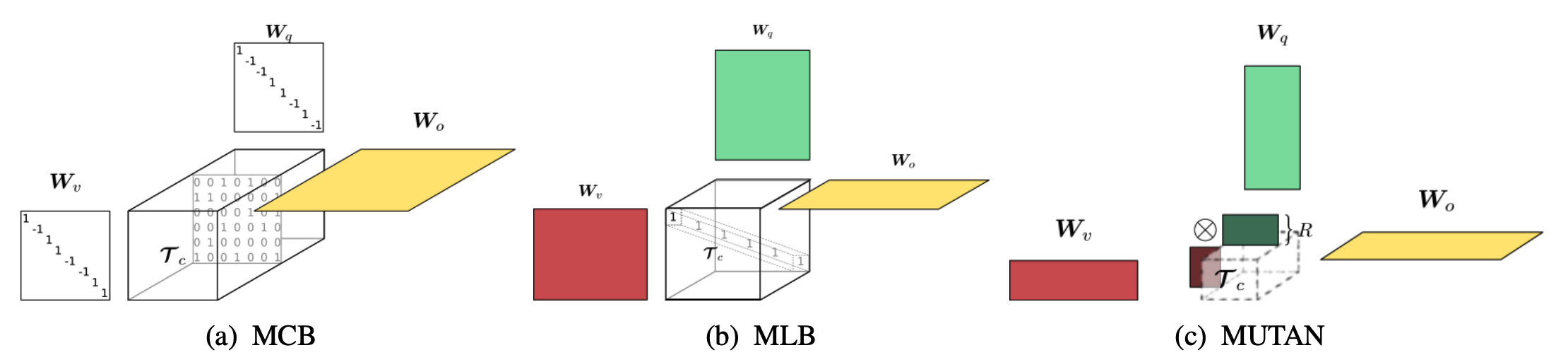

MCB and MLB can be represented with a generalized form of MUTAN.

So?

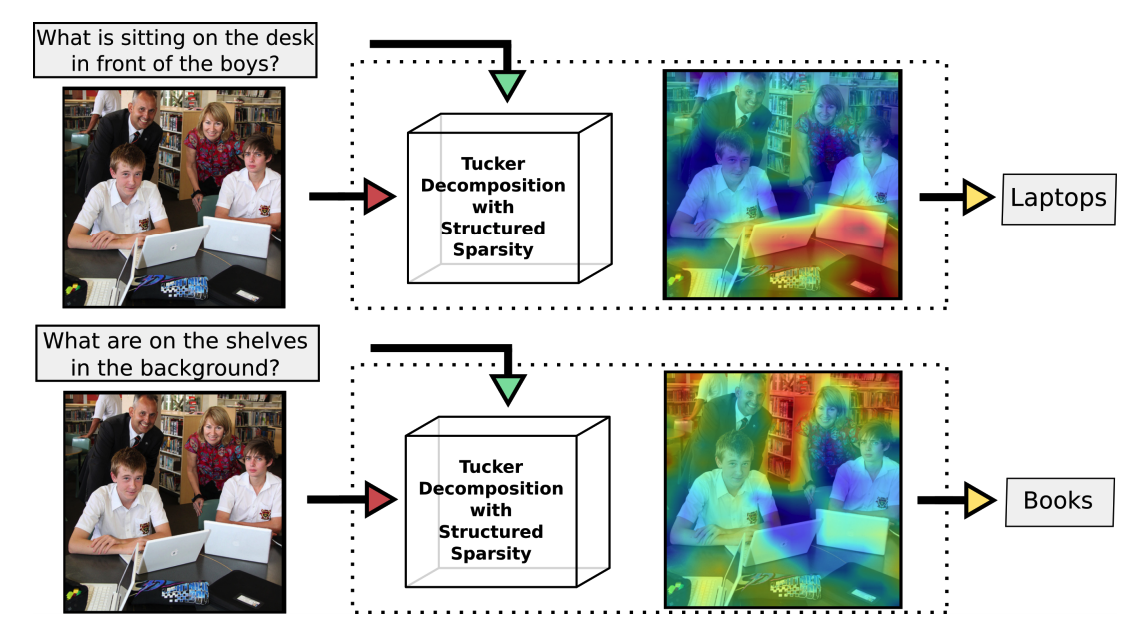
MUTAN can represent rich multimodal representation. Achieved SOTA results on VQA dataset.

Ben-Younes, Hedi, et al. “Mutan: Multimodal tucker fusion for visual question answering.” 2017 IEEE International Conference on Computer Vision (ICCV). IEEE, 2017.