WHY?

Neural network was poor at manipulating numerical information outside the range of training set.

WHAT?

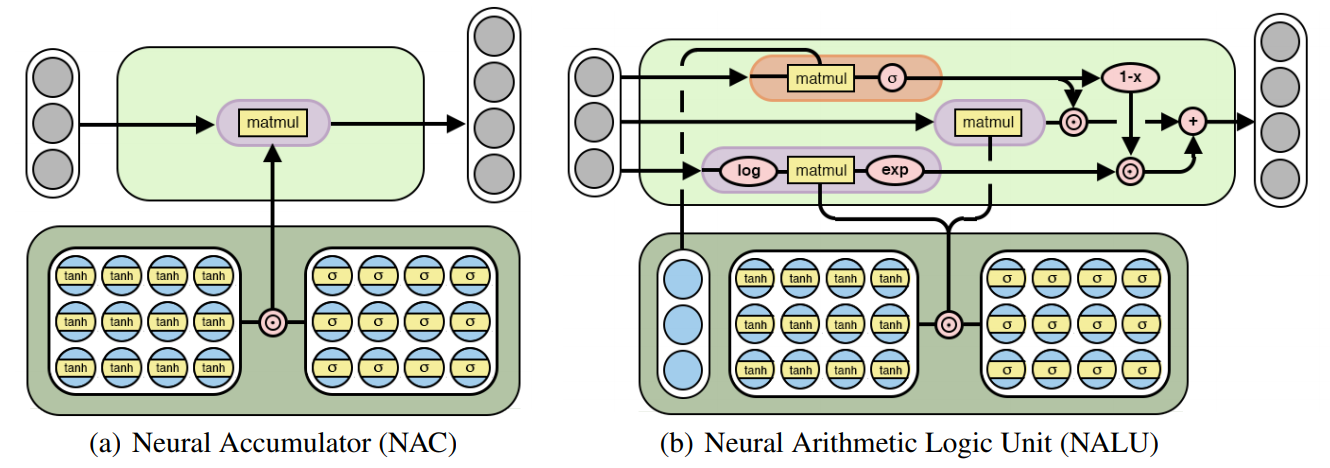
This paper suggests two models that learn to manipulate and extrapolate numbers. The first model is the neural accumulator(NAC) which accumulate the quantities in rows additively. This model is a relaxed version of linear matrix multiplication with W which consists of -1, 0 or 1.

$$\mathbf{W} = \tanh(\hat{\mathbf{W}})\odot\sigma(\hat{\mathbf{M}})\\ \mathbf{a} = \mathbf{W}\mathbf{x}$$

The second model is the neural arithmetic logic unit(NALU) which can perform multiplicative arithmetic. NALU is weighted sum of a NAC and another NAC that operates in log space.

$$\mathbf{g} = \sigma(\mathbf{G}\mathbf{x})\\ \mathbf{m} = \exp \mathbf{W}(\log(|\mathbf{x}|+\epsilon))\\ \mathbf{y} = \mathbf{g}\cdot\mathbf{a} + (1 - \mathbf{g})\cdot \mathbf{m}$$

So?

NALU successfully operated on various tasks with extrapolated numerical values including simple function learning tasks, MNIST counting and arithmetic tasks, language to number translation tasks and program evaluation task. NALU even performed well on non-numerical extrapolation task such as tracking the time in a Grid-World environment and MNIST parity prediction task.

Trask, Andrew, et al. “Neural arithmetic logic units.” Advances in Neural Information Processing Systems. 2018.