WHY?

Choosing an appropriate prior is important for VAE. This paper suggests two-layered VAE with flexible VampPrior.

WHAT?

The original variational lower-bound of VAE can be decomposed as follows.

$$\mathbb{E}_{x\sim q(x)}[\ln p(x)] \geq \mathbb{E}_{x\sim(x)}[\mathbb{E}_{q_{\phi}(z|x)}[\ln p_{\theta}(x|z)+\ln p_{\lambda}(z) - \ln q_{\phi}(z|x)]] \triangleq \mathcal{L}(\phi, \theta, \lambda) \\ = \mathbb{E}_{x \sim q(x)}[\mathbb{E}_{q_{\phi}(z|x)}[\ln p_{\theta}(x|z)]] + \mathbb{E}_{x\sim q(x)}[\mathbb{H}[q_{\phi})(z|x)]] - \mathbb{E}_{x\sim q(x)}[-\ln p_{\lambda}(z)]$$

The first component is the negative reconstruction error, the second component is the expectation of the entropy of the variational posterior, and the last component is the cross-entropy betwen the aggregated posterior and the prior. Usually the prior is given with a simple distribution such as Gaussian Normal, but a prior that optimized the ELBO can be found as the aggregated posterior.

$$max_{p_{\lambda}(z)} - \mathbb{E}_{z \sim q(z)}[=\ln p_{\lambda}(z)] + \beta (\int p_{\lambda}(z)dz -1)\\ p_{\lambda}^*(z) = \frac{1}{N}\sum_{n=1}^N q_{\phi}(z|x_n)$$

However this not only leads to overfitting, but also expensive to compute. So this paper suggests variational mixture of posteriors prior(VampPrior) that approximates the prior with a mixture of variational posteriors of pseudo-inputs. These pseudo-inputs are learned by backpropagation.

$$p_{\lambda}(z) = \frac{1}{K}\sum^K_{k=1}q_{\phi}(z|u_k)$$

In order to prevent inactive stochastic units problem, this paper suggests two-layered VAE.

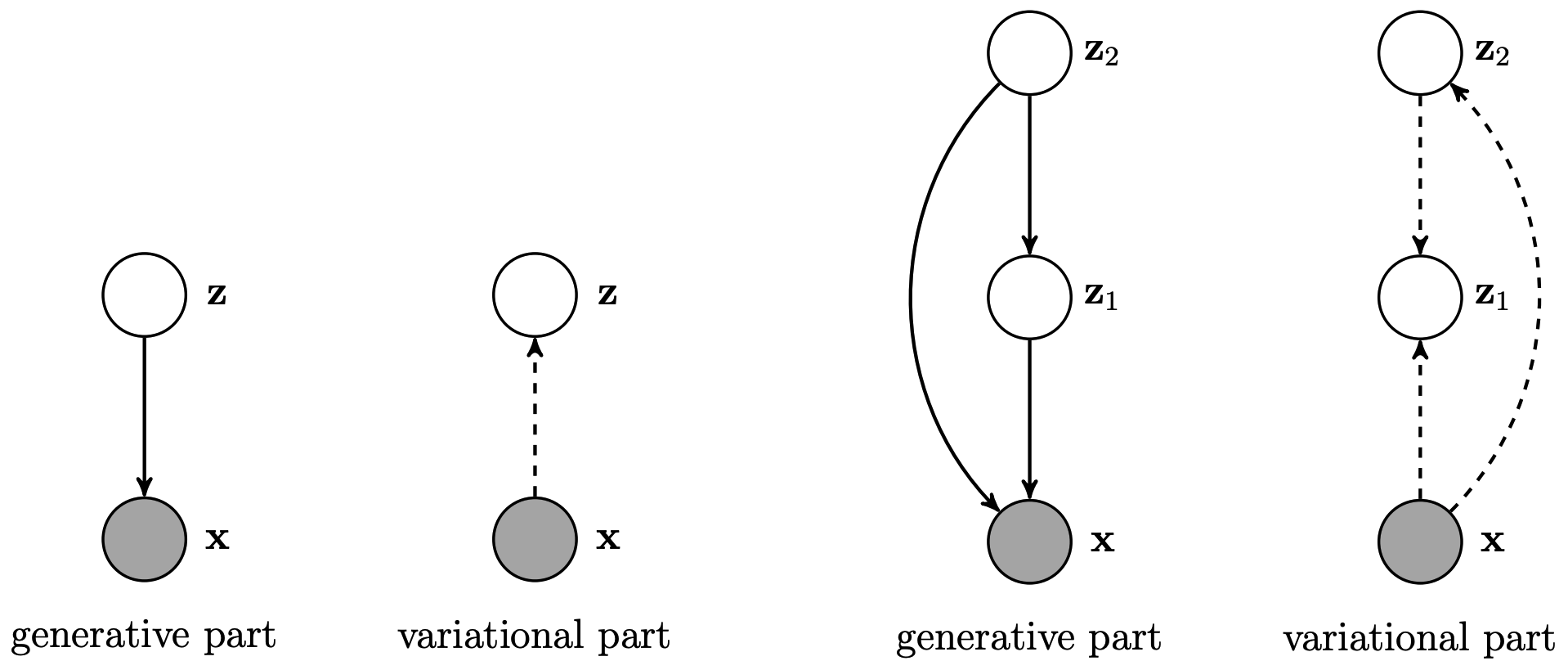
$$q_{\phi}(z_1|x, z_2) q_{\psi}(z_2|x)\\ p_{\theta}(x|z_1, z_2) p_{\lambda}(z_1|z_2)p(z_2)\\ p(z_2) = \frac{1}{K}\sum_{k=1}^K q_{\psi}(z_2|u_k)\\ p_{\lambda}(z_1|z_2) = \mathcal{N}(z_1|\mu_{\lambda}(z_2), diag(\sigma_{\lambda}^2(z_2)))\\ q_{\phi}(z_1|x, z_2) = \mathcal{N}(z_1|\mu_{\phi}(x, z_2), diag(\sigma_{\phi}^2(x, z_2)))\\ q_{\psi}(z_2|x) = \mathcal{N}(z_2|\mu_{\psi}(x), diag(\sigma_{\psi}^2(x)))$$

So?

HVAE with VampPrior achieved good results on various dataset(MNIST, dynamix MNIST, OMNIGLOT, Caltech 101 Silhouette, Frey Faces and Histopathology patches) not only in log-likelihood(LL) but also in quality reducing blurring problem in standard VAE.

Tomczak, Jakub M., and Max Welling. “VAE with a VampPrior.” arXiv preprint arXiv:1705.07120 (2017).