WHY?

Dimension of word embedding is usually determined with heuristic.

WHAT?

This paper suggests new metric to evaluate the quality of word embedding and uses it to find its optimal dimensionality. Word embedding algorithms are shown to converge to implicitly factorized PMI matrix. However, L2 loss of embedding and factorized matrix cannot be used since word embedding has unitary-invariance property which indicate word embedding is invariant to rotation. So this paper suggests Pairwise Inner Product(PIP) loss which measure relative position shifts between embeddings.

$$PIP(E) = EE^T\\ \|PIP(E_1) - PIP(E_2)\| = \|E_1 E_1^T - E_2 E_2^T\| = \sqrt{\sum_{i, j}(\langle v_i^{(1)}v_j^{(1)}\rangle - \langle v_i^{(2)}v_j^{(2)}\rangle)^2}$$

Using PIP loss, optimal dimensionality can be found that maximize the quality of embedding. This paper reported that choosing dimensionality of word embedding can be explained as bias-variance trade-off. Larger dimensionality leads to low bias but can increase estimation noise and smaller dimensionality does the opposite. Mathmathical proof was provided to show that the bias-variance trade-off captures the signal-to-noise ratio.\

So?

Using given facts, this paper provides two discovery.

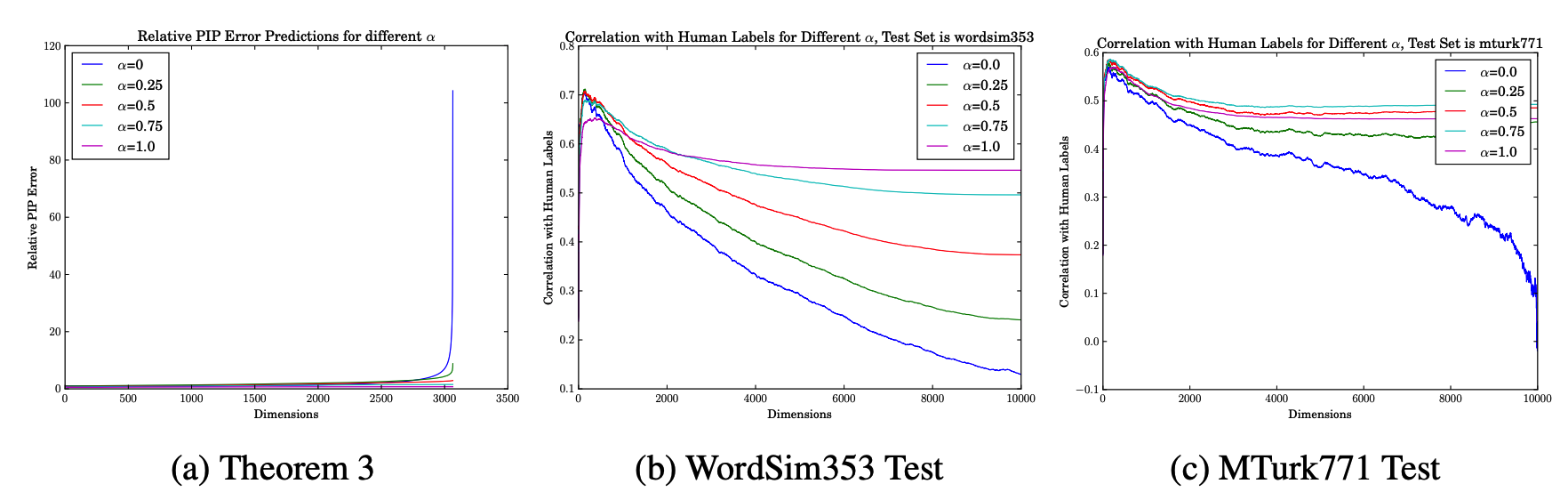
Suppose $E = U_{\cdot,1:d}D_{1:d,1:d}^{\alpha}$, larger $\alpha$ leads to robustness to over-fitting.

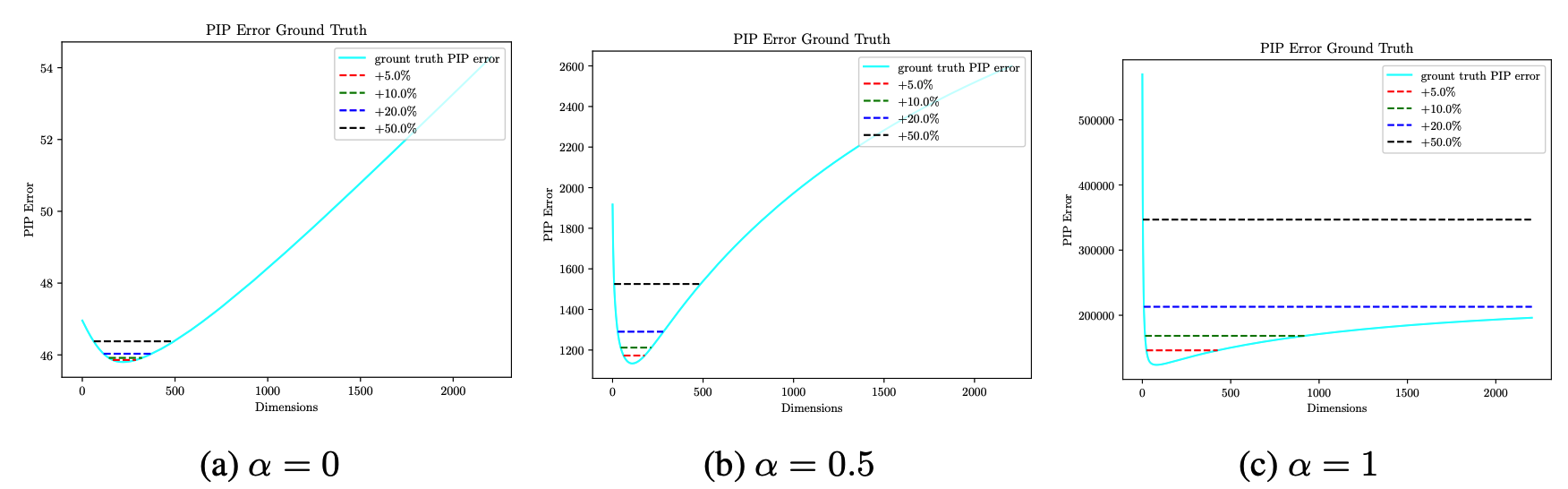
Also, optimal dimensionality can be found that minimize the PIP loss by balancing bias-variance trade-off.

Yin, Zi, and Yuanyuan Shen. “On the dimensionality of word embedding.” Advances in Neural Information Processing Systems. 2018.