WHY?

For audio source separation task, traditional approach only utilized magnitude part ignoring phase part. Previously deep complex network provided complex arithmetics via convolution.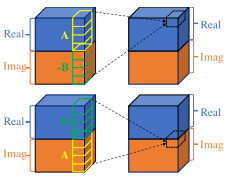

WHAT?

Deep Complex U-net modified simple DCN to better preseve audio information. First, DCU used strided complex-valued convolutional layers instead of max pooling operation. Second, complex batch normalization is used. Third, leaky CReLU is used instead of CReLU. For source separation task, DCU used complex-valued mask instead of real-valued mask.

$$\hat{Y_{t,f}} = M_{t,f}\cdot X_{t,f}\\ = (|M_{t,f}|\cdot|X_{t,f}|)\cdot e^{i(\theta_{X_{t,f}} + \theta_{M_{t,f}})}$$

The problem of complex-valued mask is that the values can range from -$\infty$ to $\infty$(Unbounded mask). Unbounded mask may capture any form of appropriate mask, but empirically proved that the good optimization is difficult.

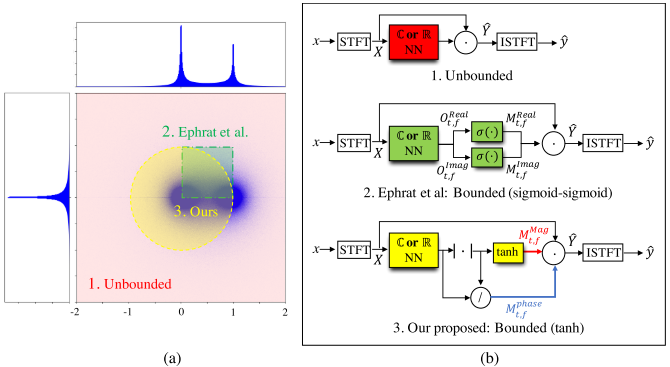
Previous work suggested sigmoid activation for each of real and imaginary part. However, seeing the distribution of appropriate mask, this activation can capture very limited area. DCU suggest polar-coordinate-wise masking to keep the mask bounded in a unit-circle in complex-space.

$$M_{t,f} = |M_{t,f}|\cdot e^{i\theta_{M_{t,f}}}= M_{t,f}^{mag}\cdot M_{t,f}^{phase}\\ M_{t,f}^{mag} = tanh(|O_{t,f}|), M_{t,f}^{phase} = O_{t,f}/|O_{t,f}|$$

Since former MSE losses(Spectrogram-MSE, Wave-MSE) did not correlated with evaluation measures, DCU proposed weighted-SDR losses. Source-to-distortion ratio(SDR) represent the distortion ratio of reconstruted audio.

$$max_{\hat{y}} SDR(y, \hat{y}) := max_{\hat{y}} \frac{<y, \hat{y}>^2}{\|y\|^2\|\hat{y}\|^2 - <y, \hat{y}>^2}\\ \propto min_{\hat{y}}\frac{\|y\|^2\|\hat{y}\|^2}{<y, \hat{y}>^2} - frac{<y, \hat{y}>^2}{<y, \hat{y}>^2}\\ \propto min_{\hat{y}}\frac{\|\hat{y}\|^2}{<y, \hat{y}>^2}$$

To prevent the zero division and bound the loss to -1 to 1, weighted-SDR loss is proposed.

$$loss_{SDR}(y, \hat{y}) := \frac{<y, \hat{y}>}{\|y\|\|\hat{y}\|+\epsilon}\\ loss_{wSDR}(x, y, \hat{y}) := \alpha loss_{SDR}(y, \hat{y}) + (1-\alpha)loss_{SDR}(z, \hat{z}) + 1\\ \alpha = \frac{\|y\|^2}{\|\hat{y}\|^2+\|z\|^2}\\ z = x-y\\ \hat{z} = x-\hat{y}$$

So?

DCU achieved state-of-the-art result in CSIG, CBAK, COVL, PESQ, and SSNR compared to SEGAN, Wavenet, MMSE-GAN and Deep Feature Loss.

Critic

Incredible application of complex-network!

Not disclosed yet