WHY?

Gaussian process has several advantages. Based on robust statistical assumptions, GP does not require expensive training phase and can represent uncertainty of unobserved areas. However, HP is computationally expensive. Neural process tried to combine the best of Gaussian process and neural network.

WHAT?

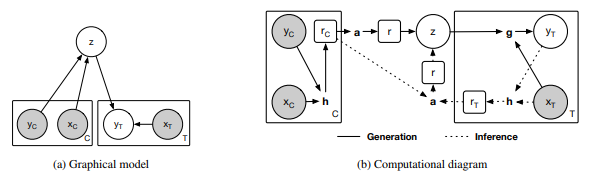
Neural process satisfy two condtions of stochastic process: exchageability and consistency. To represent GP with neural network, stochastic process F can be parameterised by random vector z.

$$F(x) = g(x, z)\\ p(z, y_{1:n}|x_{1:n}) = p(z)\prod^n_{i=1} N(y_i|g(x_i, z), \sigma^2)$$

We can split the dataset into a context set $x_{1:m}, y_{1:m}$ and a target set $x_{m+1:n}, y_{m+1:n}$. Variational inference is used to estimate the log likelihood, and intractable conditional prior $$p(z

x_{1:m}, y_{1:m})$$ is approximated using another variational inference.

$$\log p(y_{m+1:n}|x_{1:n}, y_{1:m}) \geq \mathbb{E}_{q(z|x_{1:n},y_{1:n})}[\sum^n_{i=m+1}\log p(y_i|z, x_i) + \log\frac{p(z|x_{1:m}, y_{1:m})}{q(z|x_{1:n},y_{1:n})}] \geq \\ \mathbb{E}_{q(z|x_{1:n},y_{1:n})}[\sum^n_{i=m+1}\log p(y_i|z, x_i) + \log\frac{q(z|x_{1:m}, y_{1:m})}{q(z|x_{1:n},y_{1:n})}]$$

To train this model to represent the distribution of functions, dataset have to be divided into context points and target points. Encoder parameterized with a neural network takes pairs of context points($x_i, y_i$) and produce each representation $r_i$. In order to represent order-invariant global representation r, aggregator takes means of each representation.

$$z\sim N(\mu(r), I\sigma(r))\\ r = a(r_i) = \frac{1}{n}\sum_{i=1}^n r_i$$

A conditional decoder takes a global latent variable and new target locations to make prediction.

So?

NP showed fine performance on 1-D function regression, 2-D function regression, black-boc optimiation with thompson sampling, and contextual bandits.

Critic

Frankly, I think I need to implement this in order to fully understand this.

Garnelo, Marta, et al. “Neural processes.” arXiv preprint arXiv:1807.01622 (2018).