WHY?

Learning directed generative model is difficult.

WHAT?

Deep AutoRegressive Network(DARN) models images with hierarchical, autoregressive hidden layers.DARN has three components: a encoder q(H|X), a decoder prior p(H), and a decoder conditional p(X|H). We consider all the latent variables (h) in this model are binary. The decoder prior is an autoregressive model. The conditional probabilities can be modeled with simple logistic regressions.

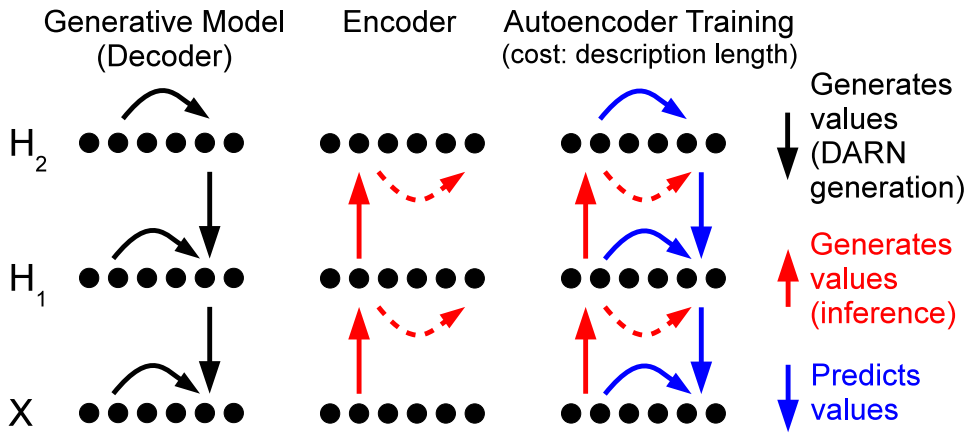
$$p(h) = \prod_{j=1}^{n_h}p(h_j|h_{1:j-1})\\ p(H_j = 1|h_{1:j-1}) = \sigma(W_j^(H)\cdot h_{1:j-1} + b_j^{H})\\ p(x|h) = \prod_{j=1}^{n_h}p(x_j|x_{1:j-1}, h)\\ p(X_j = 1|x_{1:j-1}, h) = \sigma(W_j^(X|H)\cdot (x_{1:j-1},h) + b_j^{X|H})\\ q(h|x) = \prod_{j=1}^{n_h}q(h_j|h_{1:j-1}, x)\\ q(H_j = 1|h_{1:j-1}, x) = \sigma(W_j^(H|X)\cdot x + b_j^{H|X})$$

We can make deeper architectures of DARN by adding additional stochastic hidden layers, additional deterministic hidden layers, and additional kinds of autoregressivity such as NADE.

$$p(H^{(l)}|H^{(l+1)}) = \prod_{j=1}^{n_h^{(l)}} p(H_j^{(l)}|H_{1:j-1}^{(l)}, H^{(l+1)})\\ q(H^{(k)}|H^{(k-1)}) = \prod_{j=1}^{n_h^{(k)}} q(H_j^{(k)}|H_{1:j-1}^{(k)}, H^{(k-1)})\\ d^{l} = tanh(Uh^{(l+1)})\\ p(H_j^{l} = 1 | h^{(l)}_{1:j-1}, h^{(l+1)}) = \sigma(W_j^{(H)}\cdot (h^{(l)}_{1:j-1},d^{l}) + b_j^{H})$$

The cost function is defined with minimum description length (MDL), which is equivalent to Helmholtz variational free energy.

$$L(x) = \sum^h q(h|x)(L(h) + L(x|h))\\ = -\sum^h q(h|x)(log_2p(x,h) - log_2q(h|x))\\ = \sum_{h_1=0}^1q(h_1|x) ... \sum_{h_{n_h}=0}^1q(h_{n_h}|h_{1:n_h-1},x)\prod(log_2q(h|x) - log_2p(x,h))$$

Calculating the derivative of the cost function is intractable, so MC approximation is used to estimate the gradient.

Laplacian Pyramid Framework is used for restoring compressed image. When a image is compressed to smaller size, it would lose information of high-resolution image so that simply enlarging the image would not be enough to restore original data. Laplacian pyramid framework save the differences between enlarged low resolution image and high resolution image at each stage.

So?

DARN performed better than RBM, FVSBN, NDAE in log likelihood in UCI and binarised MNIST dataset.

Critic

Backpropagation seems inconvenient.

Gregor, Karol, et al. “Deep autoregressive networks.” arXiv preprint arXiv:1310.8499 (2013).