WHY?

Gradient descent methods depend on the first order gradient of a loss function wrt parameters. However, the second order gradient(Hessian) is often neglected.

WHAT?

This paper explored exact Hessian prodect of neural network (after convergence) and discovered that the eigenvalue of Hessian is separated into two groups: 0s and large, positive values (singular). 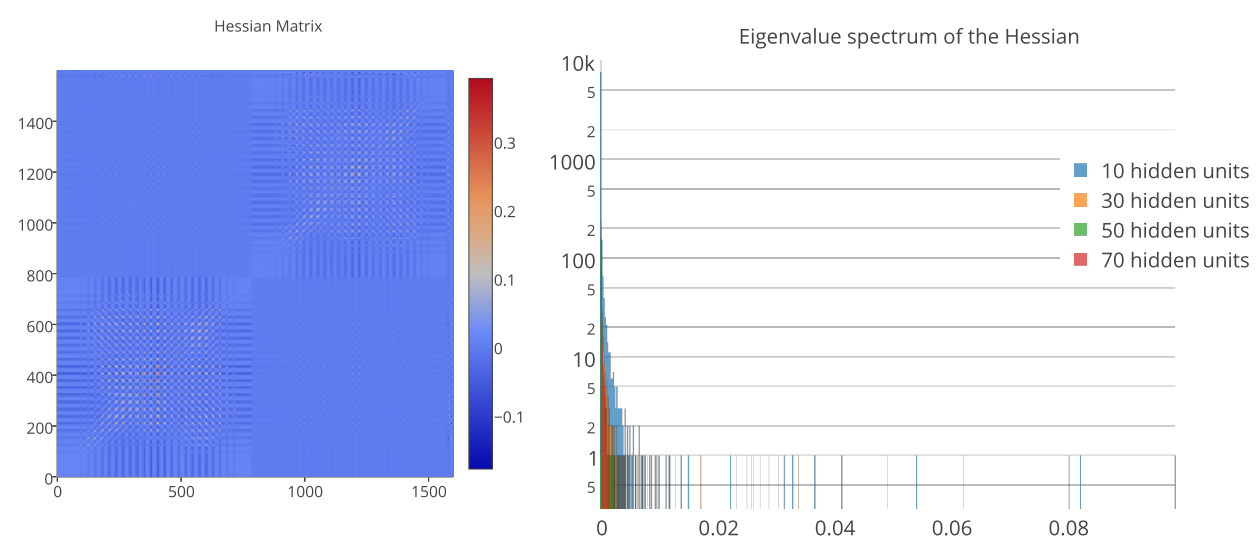This property did not depend on the loss function, or the choice of initial points. Varying the parameters of models and datas, this paper observed that the bulk of the eigenvalues depend on the architecture while top discrete eigenvalues depend on data.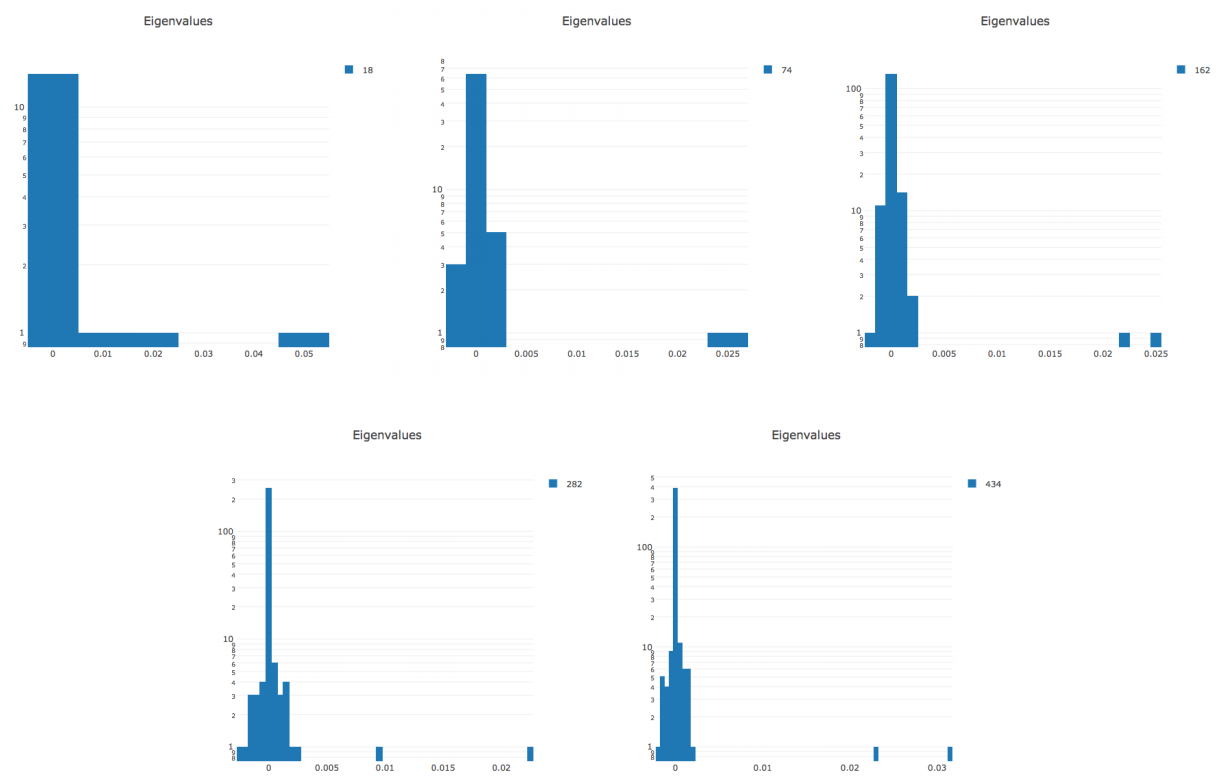

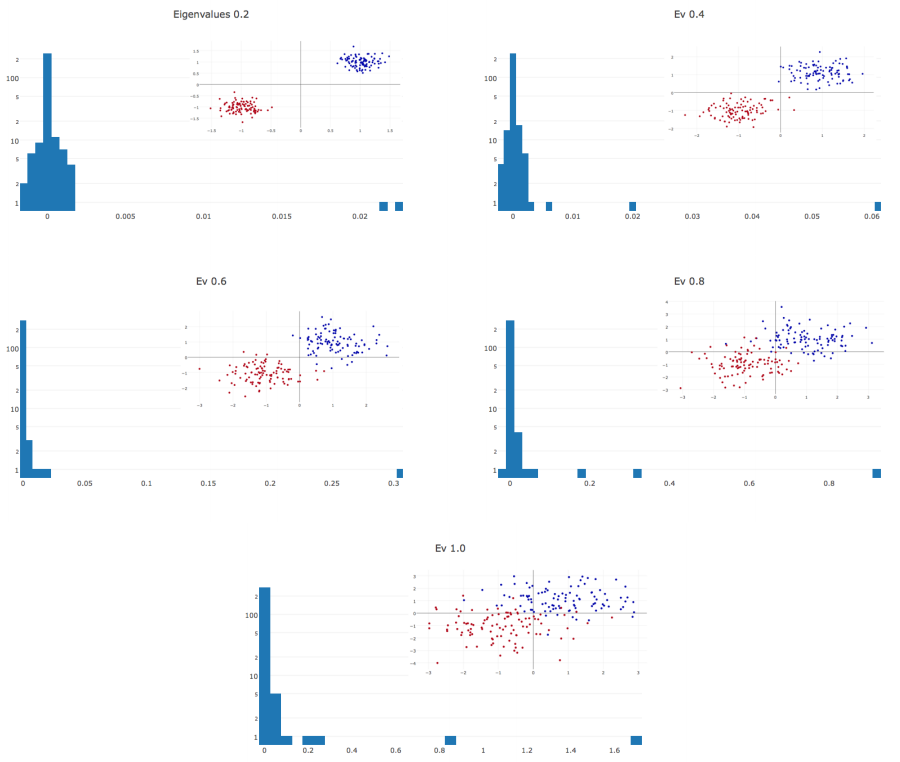
So?

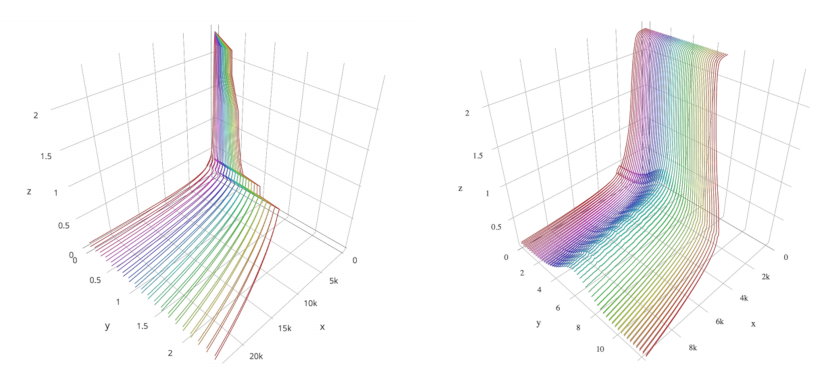The property of Hessian provides useful information about landscape.

Critic

Deeper discussion about the property would be nicer.

Sagun, Levent, Leon Bottou, and Yann LeCun. “Eigenvalues of the Hessian in Deep Learning: Singularity and Beyond.” arXiv preprint arXiv:1611.07476 (2016).