WHY?

Efficient exploration of agent in reinforcement learning is an important issue. Conventional exploration heuristics includes $\epsilon$-greedy for DQN and entropy reward for A3C.

WHAT?

NoisyNet is a neural network whose parameters are replaced with a parametric function of the noise. 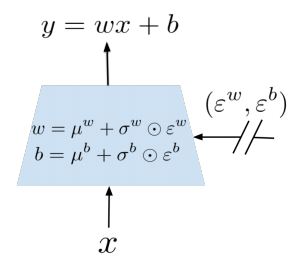$\theta =^{def} \mu + \Sigma \odot \epsilon\\ y =^{def} (\mu^w + \sigma^w \odot \epsilon^w)x + \mu^b = \sigma^b \odot \epsilon^b\\$ There are two options for noise: Independent Gaussian noise and Factorised Gaussian noise. Independent Gaussian noise insert noise per weight(pq + q per layer), but factorised Gaussian insert noise per each input and output(p + q per layer). Since factorised Gaussian requires less random variables generation, it can be used for a single thread agents DQN and independent noise can be used for the distributed A3C. The loss of Noisy Network applied to DQN is as follows.
$\mathcal{E}[\mathcal{E}_{(x, a, r, y)\sim D}[r = \gamma Q(y, b^*(y), \epsilon'; \zeta^-) - Q(y, a, \epsilon'; \zeta)]]\\ b^*(y) = argmax_{b\in \mathcal{A}}Q(y, b(y), \epsilon''; \zeta)$

So?

NoisyNet-DQN/Dueling/A3C showed overall improved performance over models without noise. 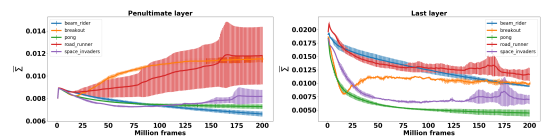The evolution of $\sigma$ differed significantly by the tasks.

Critic

I’m quite surprised that this can actually work. More experiments on when the agent choose to explore more would be helpful.

Fortunato, Meire, et al. “Noisy networks for exploration.” arXiv preprint arXiv:1706.10295 (2017).