WHY?

There had been little study on learning representation that focus on clustering.

WHAT?

Deep Embedding Clustering(DEC) consists of two phases: parameter initialization with a deep autoencoder and (2) parameter optimization. This paper first describe the second phase. Assume encoder and inital cluster centroids are given, two steps are alternated to improve clustering: 1) compute soft assignment of embedded points to centroids, and 2) update encoder and refine centroids.
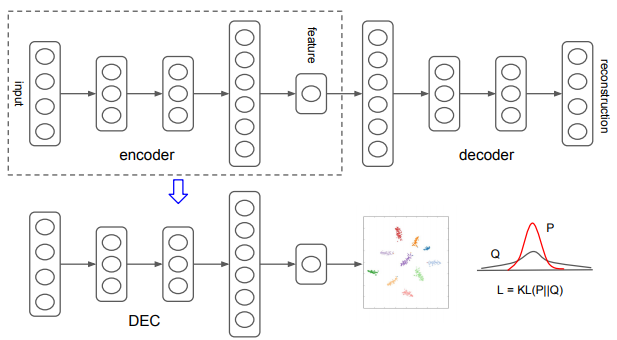Student’s t-distriution is used as kernel for soft assignment. An auxiliary distribution p is designed to help learn from high confidence assignments. KL-divergence between soft assignment and auxiliary distribution is minimize by updating encoder and centroids. $q_{ij} = \frac{(1+\|z_i - \mu_j\|^2/\alpha)^{-\frac{\alpha+1}{2}}}{\sum_{j'}(1+\|z_i - \mu_j\|^2/\alpha)^{-\frac{\alpha+1}{2}}}\\ p_{ij} = \frac{q_{ij}^2/f_j}{\sum_{j'}q_{ij'}^2/f_{j'}}, f_j = \sum_i q_{ij}\\ L = KL(P\|Q) = \sum_i \sum_j p_ij \log \frac{p_{ij}}{q_{ij}}$ Trained Stacked Autoencoder(SAE) with denoising autoencoder for each layer is used to initialize the embeddings. Initial centroids are determined by k-means clustering of initial embeddings.

So?

DEC outperformed many clustering methods including k-means, LDMGI, and SEC in unsupervised clustering task of MNIST, STL-10, and Reuters. 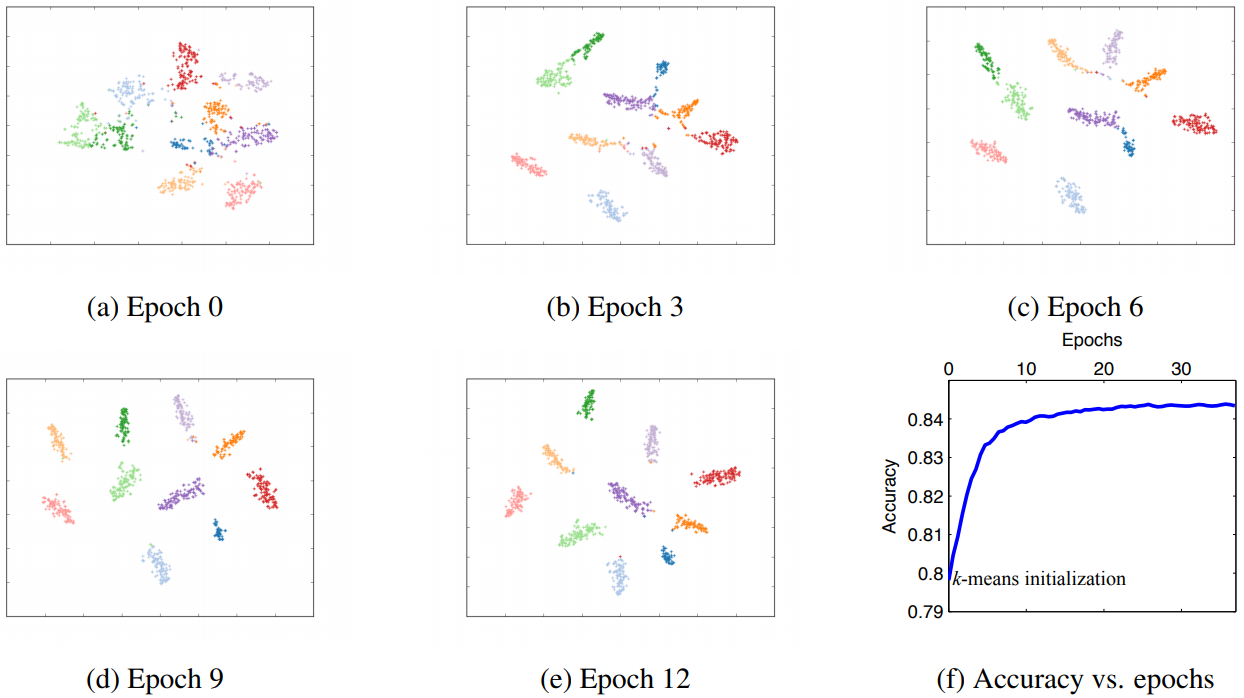Visualization verified that embeddings are well separated.

Critic

I like the idea to learn representation jointly with clustering, auxiliary target distribution seems like quite aritrary to me.

Xie, Junyuan, Ross Girshick, and Ali Farhadi. “Unsupervised deep embedding for clustering analysis.” International conference on machine learning. 2016.