WHY?

Estimating the distribution of data can help solving various predictive taskes. Approximately three approaches are available: Directed graphical models, undirected graphical models, and density estimation using autoregressive models and feed-forward neural network (NADE).

WHAT?

Autoregressive generative model of data consists of D conditionals. NADE use feed-forward neural network to model each conditionals. First, we assume that x is binary. W and c are shared. $p(x) = \prod_{d=1}^D p(x_{O_d})|x_{O_{<d}})\\ p(x_{o_d}|x_{o_{<d}}) = sigm(V_{o_d,\cdot}h_d + b_{o_d})\\ h_d = sigm(W_{\cdot, o<d}x_{o<d} + c)$ Computation cost is O(H) since W and c are shared. $a_d = W_{\cdot, o_{<d}} + c\\ h_1 = sigm(a_1), where a_1 = c\\ h_d = sigm(a_d), where a_d = W_{\cdot, o_{<d}}x_{o_{<d}} + c = W_{\cdot, o_{d-1}}x_{o_{d-1}} + a_{d-1}$ NADE can be trained by maximum likelihood. Algorithm is as follows. 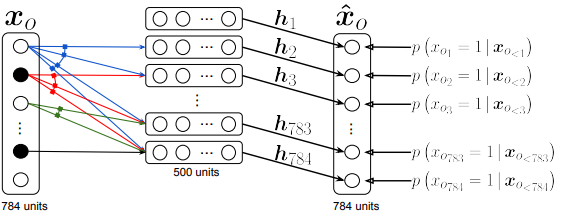We can extend NADE with other options. RNADE extends binary value x to real value, estimating rhe conditionals as Gaussian mixture. Orderless deep Nade mix the order of input using binary mask and concatenate mask as input to get conditionals. 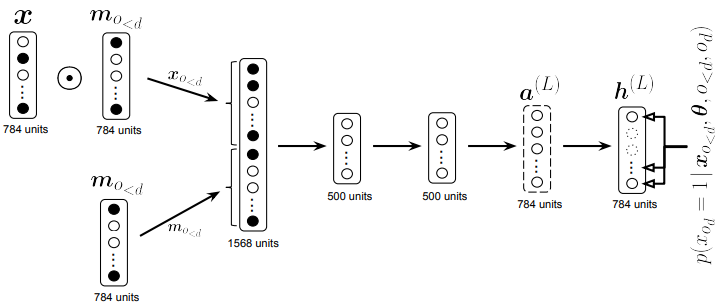ConvNADE use convolution filters as W and stacks L layers. 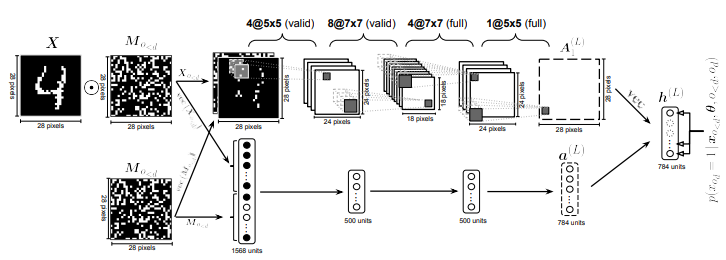We can combine ConvNADE with deep NADE.

So?

This paper performed extensive experiments with NADE. NADE was able to capture fairly good distribution of MNIST.

Critic

Autoregressive framework is nice. However, I think this can be combined with hierarchical structure of features.

Uria, Benigno, et al. “Neural autoregressive distribution estimation.” The Journal of Machine Learning Research 17.1 (2016): 7184-7220.