WHY?

Many machine learning problems involves loss function that contains random variables. To perform backpropagation, estimating gradient of the loss function is required.

WHAT?

This paper tried to formalize the computation of gradient of loss function with computation graphs. Assume we want to compute $\frac{\partial}{\partial\theta}\mathbb{E}_x[f(x)]$. There are two differnt way that random variable x can be influenced by $\theta$.

1. Score Function Estimator
   If probability distribution is parametrized by $\theta$, the gradient can be estimated with score function estimator.
   $\frac{\partial}{\partial\theta}\mathbb{E}_x[f(x)] = \mathbb{E}_x[f(x)\frac{\partial}{\partial\theta}\log p(x; \theta)]$
   Score function extimator is also known as likelihood ratio estimator, or REINFORCE.
2. Pathwise derivative
   If x is deterministically influenced by another random variable z which is influenced by $\theta$ the gradient can be estimated with pathwise derivative.
   $\frac{\partial}{\partial\theta}\mathbb{E}_x[f(x)] = \mathbb{E}_z[\frac{\partial}{\partial\theta}f(x(z, \theta))]$
   If $\theta$ appear both in the probability distribution and inside expectation,
   $\frac{\partial}{\partial\theta}\mathbb{E}_{z\sim p(\cdot;\theta)}[f(x(z,\theta))] = \mathbb{E}_{z\sim p(\cdot;\theta)} [\frac{\partial}{\partial\theta}f(x(z,\theta)) + (\frac{\partial}{\partial\theta}\log p(z;\theta))f(x(z,\theta))]$
   To formallize this with directed acyclic graph, this paper represent deterministic nodes with squares and stochastic nodes with circles.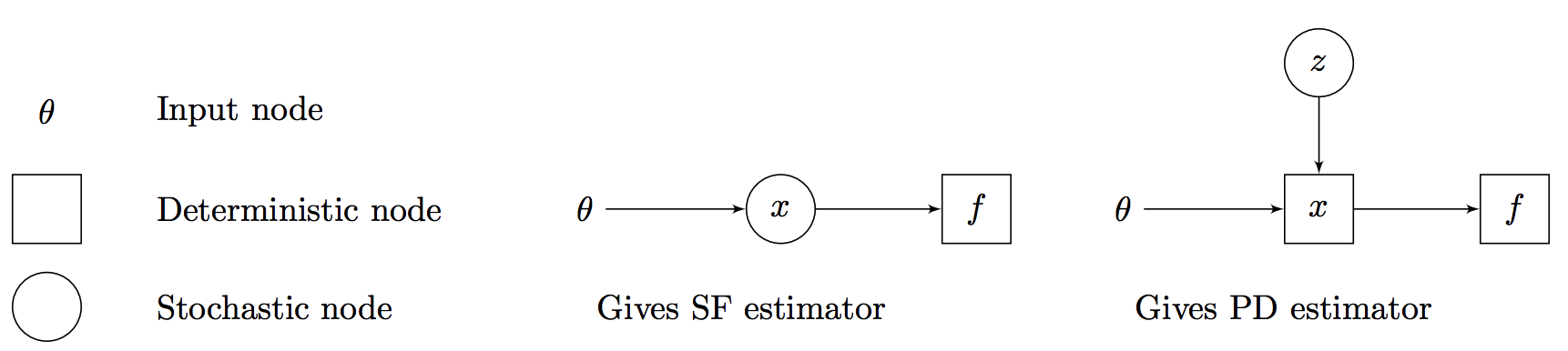 Some example can be shown as below. Further notation can be defined as below. Given differentiability requirements hold, the gradient of sum of costs can be represented as two equivalent equations. 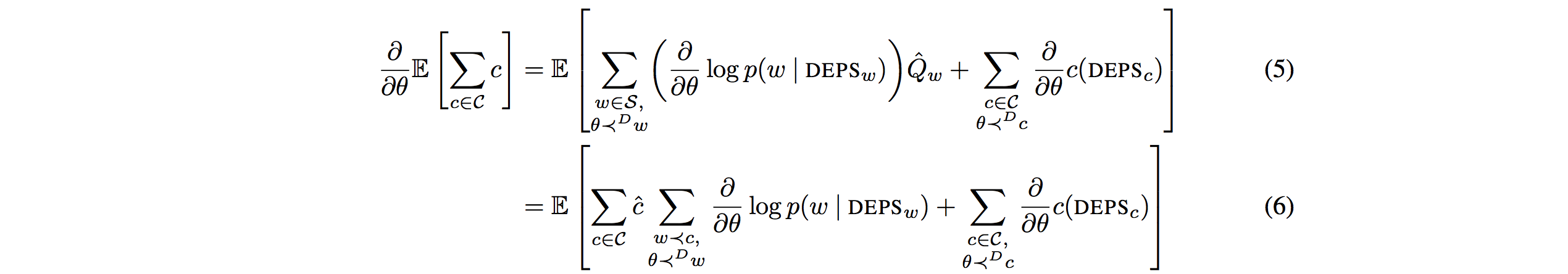This paper suggest surrogate loss function which convert the stochastic graphs to deterministic graphs from equation above.
   $\frac{\partial}{\partial\theta}\mathbb{E}[\Sigma_{c\in C}c] = E[\frac{\partial}{\partial\theta} L(\Theta, S)]\\ L(\Theta,S) := \Sigma_w\log p(w|DEPS_w)\hat{Q}_w + \Sigma_{c\in C}c(DEPS_c)$ To reduce the variance of score function estimator we can subtract the baseline estimate of the function.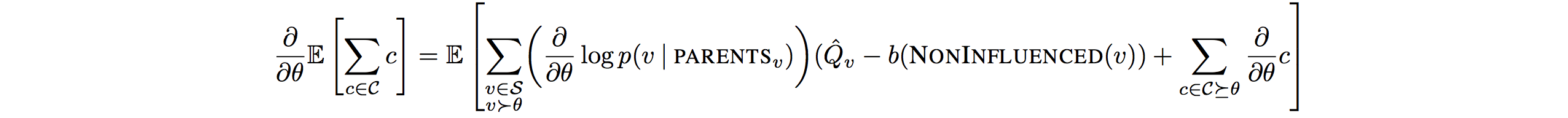 Algorithm is as below.

Critic

Great summary and clean formalation of getting gradient of function with stochatic variables.

Schulman, John, et al. “Gradient estimation using stochastic computation graphs.” Advances in Neural Information Processing Systems. 2015.