WHY?

This paper wanted to catch non-linear dynamics of the object in video.

WHAT?

KVAE(Kalman Variational Autoencoder) combined Kalman filter with VAE to model dynamic latent variables. 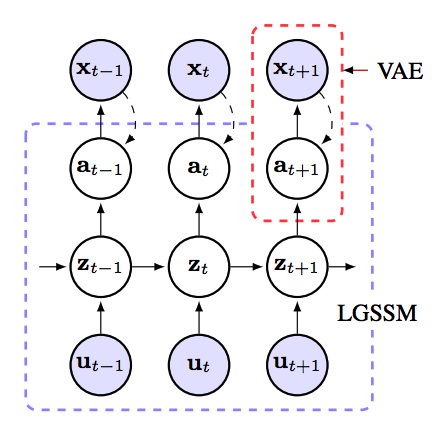Linear Gaussian state space models are used to model Kalman filter and stable latent variables of the variational autoencoder. Matrices $\gamma_t = [A_t, B_t, C_t]$ are the state transition, control and emission matrices at time t and Q and R are the covariances matrices of process and measurement noise. Using Kalman filter, we can estimate the $p(z_t|a_{1:t}, u_{1:t})$ and $p(z_t|a, u)$ exactly. $p_{\gamma_t}(z_t|z_{t-1}, u_t) = N(z_t; A_tz_{t-1} + B_t u_t, Q), p_{\gamma_t}(a_t|z_t) = N(a_t;C_t z_t, R)\\ p_{\gamma_t}(a,z|u)=p_{\gamma_t}(a|z)p_{\gamma_t}(z|u)$ In generative process, joint density of KVAE factorizes as $p(x, a, z|u) = p_{\theta}(x|a)p_{\gamma}(a|z)p_{\gamma}(z|u)$. In inference process, $\theta$ and $\gamma$ are learned to maxmize the log likelihood $log{\theta\gamma}(x|u)$. Since we can estimate the $p(z_t|a_{1:t}, u_{1:t})$ and $p(z_t|a, u)$ exactly, the variational lowerbound can be rewritten ad below. This lowerbound can be estimated through Monte Carlo method. $F(\theta, \gamma, \phi) = E_{q_\phi (a|x)}[log\frac{p_{\theta}}{q_{\phi}(a|x)} + E_{p_{\gamma}(z|a,u)}[log\frac{p_{\gamma}(a|z)p_{\gamma}(z|u)}{p_{\gamma}(z|a,u)}]]\\ \hat{F}(\theta, \gamma, \phi) = \frac{1}{I}\Sigma_i log p_{\theta}(x|\tilde{a}^{(i)}) + log p_{\gamma}(\tilde{a}^{(i)}, \tilde{z}^{(i)}|u) - log q_{\phi}(\tilde{a}^{(i)} |x) - log p_{\gamma}(\tilde{z}^{(i)}| \tilde{a}^{(i)},u)$ $a_t$ represent the dynamics but it may not always transform linearly. Therefore, this paper suggests Dynamics parameter network which linearly combines the $\gamma$ with all the previous $\gamma$ weighted by $\alpha$ estimated using LSTM.

So?

KVAE performed better in imputing missing data in Bouncing ball and got higher ELBO in Pendulum experiment.

Critic

Good to know about Kalman filter.

Fraccaro, Marco, et al. “A disentangled recognition and nonlinear dynamics model for unsupervised learning.” Advances in Neural Information Processing Systems. 2017.