WHY?

Most of deep directed latent variable models including VAE try to maximize the marginal likelihood by maximizing the Evidence Lower Bound(ELBO). However, marginal likelihood is not sufficient to represent the performance of the model.

WHAT?

Instead of marginal likelihood, this paper suggest to measure the information between the observed X and the latent Z with variational lowerbound and upperbound. $I_e(X;Z) = \iint dx dz p_e(x,z)log \frac{p_e(x,z)}{p^*(x)p_e(z)}\\ H - D \leq I_e(X; Z) \leq R\\ H \equiv -\int dx p^*(x)log p^*(x)\\ D \equiv -\int dx p^*(x) \int dz e(z|x)log d(x|z)\\ R \equiv \int dx p^*(x) \int dz e(z|x)log \frac{e(z|x)}{m(z)}$ H is data entropy, D is the distortion which is equivalent to reconstruction negative log likelihood, and R is the rate which is equivalent to average KL divergence. Hyperparameter in beta-VAE turned out to be representing the ratio between R and D. The relationship between distortion and rate can be drawn as following RD-plane. 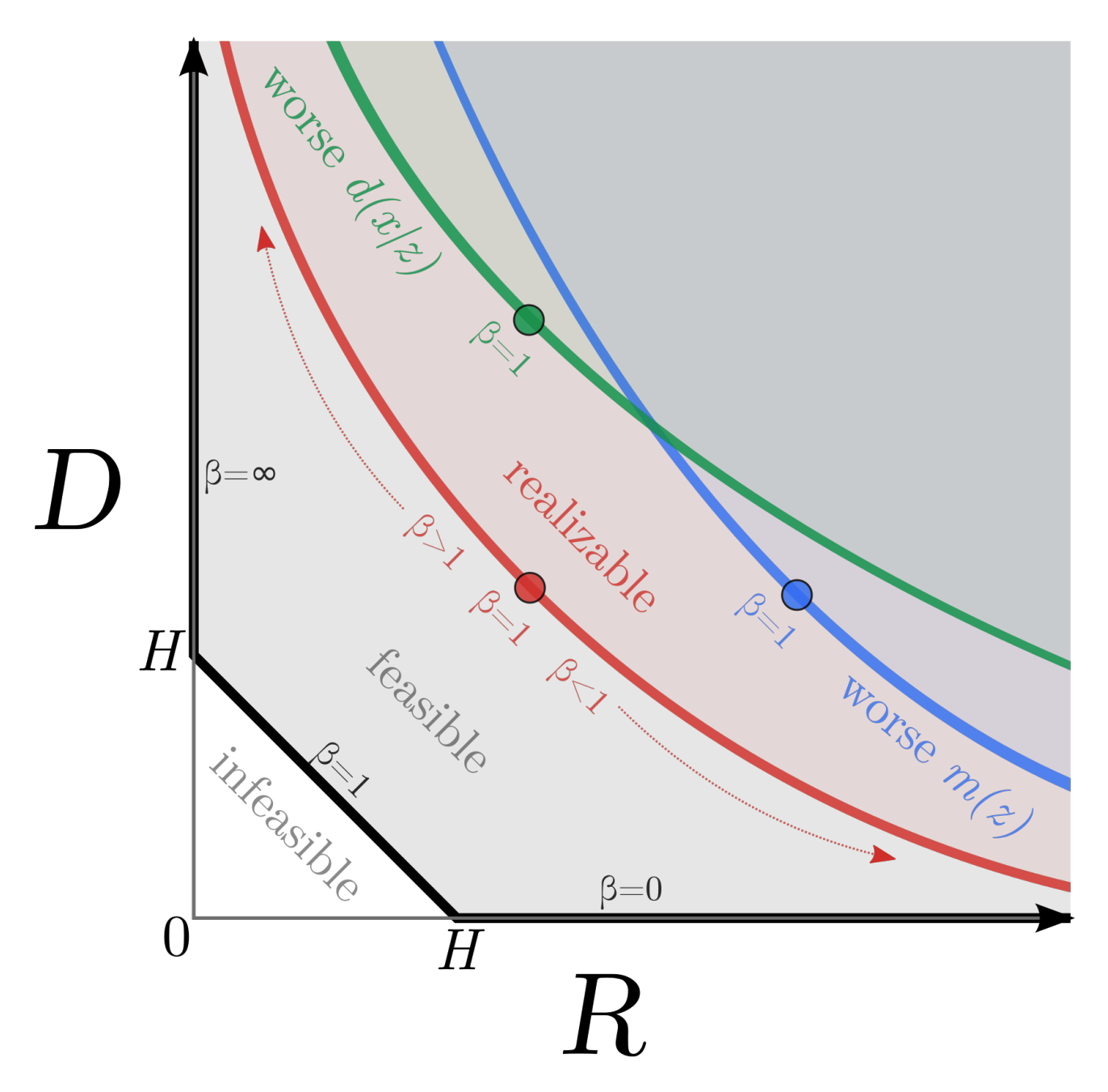High R with low D implies that the encoder did not fit to the prior so that latent representation of data is expressive but fail to generate samples with assumed prior. On the other hand, High D with low R implies that encoder fit too much to the prior so that latent representation fail to contain sufficient information (Auto-decoding). As seen in RD-plane, the performance of models with the same ELBO may vary with the ratio between distortion and rate. This paper points out that previous models minimize ELBO by supressing R, but least amount of information in R(entropy of data) is needed for desired representation. So this paper suggests to reduce the KL penalty term($\beta$) for fix to data entropy if available.
First, this paper compared normal VAE with target rate model with toy dataset with known parameters. Second, the author compared models of varying ELBO and R and D ratio.

So?

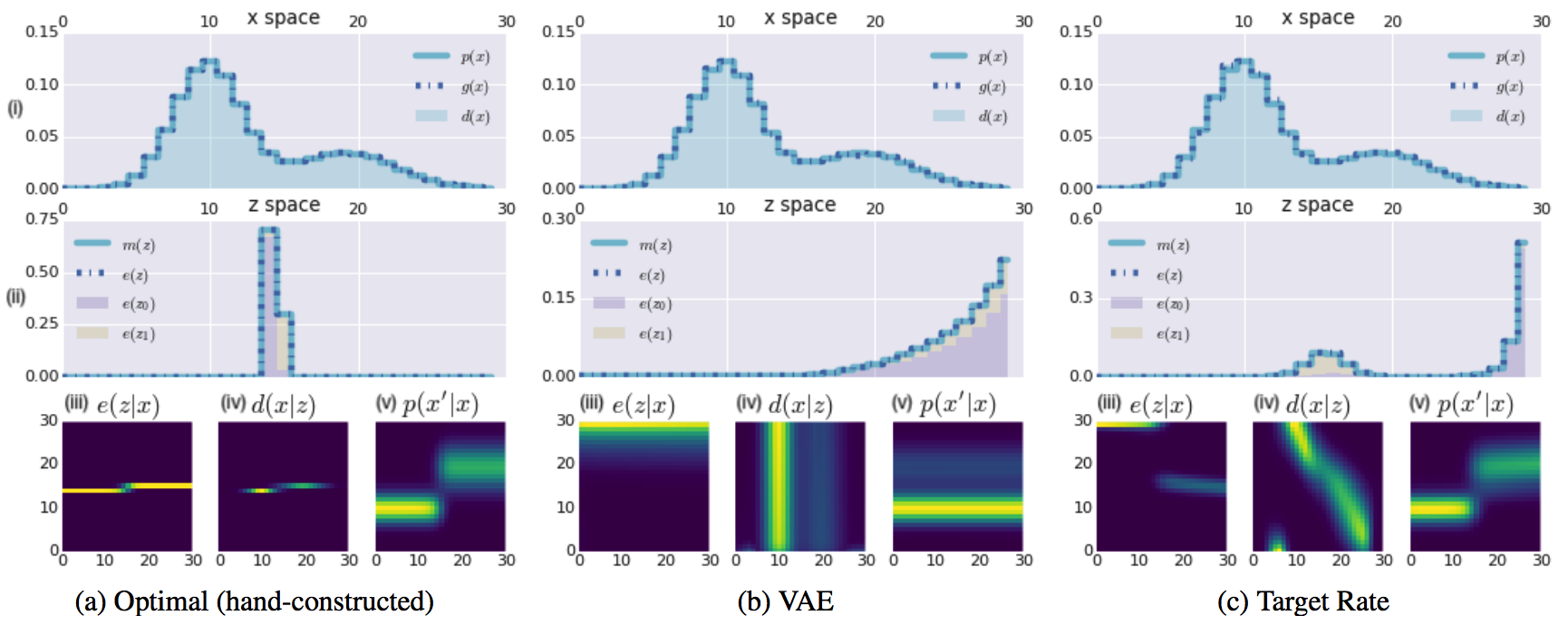VAE failed to catch the multimodality of z space by reducing R to near zero thus failing to reconstruct. However, model with target rate succedded in catching multimodality of z space and reconstructed well. 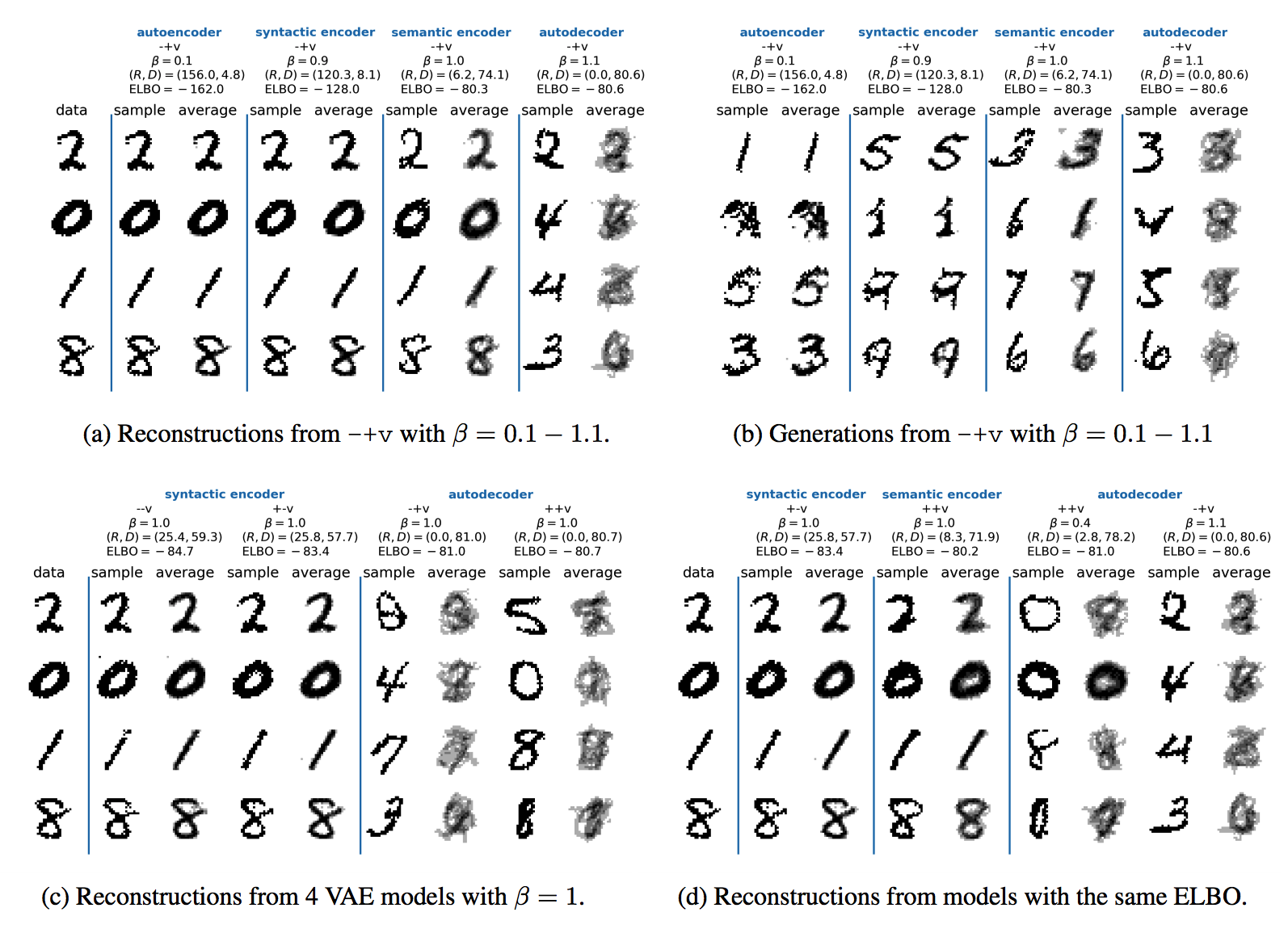By the ratio of R and D, the models can be categorized in to 4 categories: Auto-encoder, syntactic encoder, semantic encoder and auto decoder. these catergories shows varying performance as described above. Even the same ELBO with the varying ratio shows extremely varying performance.

Critic

Amazingly pointed out the critical drawback of all the previous VAE models. Description was easily understanable and the experiments were brilliant.

Alemi, Alexander A., et al. “An Information-Theoretic Analysis of Deep Latent-Variable Models.” arXiv preprint arXiv:1711.00464 (2017).