WHY?

In VAE framework, the quality of the generation relies on the expressiveness of inference model. Restricting hidden variables to Gaussian distribution with KL divergence limits the expressiveness of the model.

WHAT?

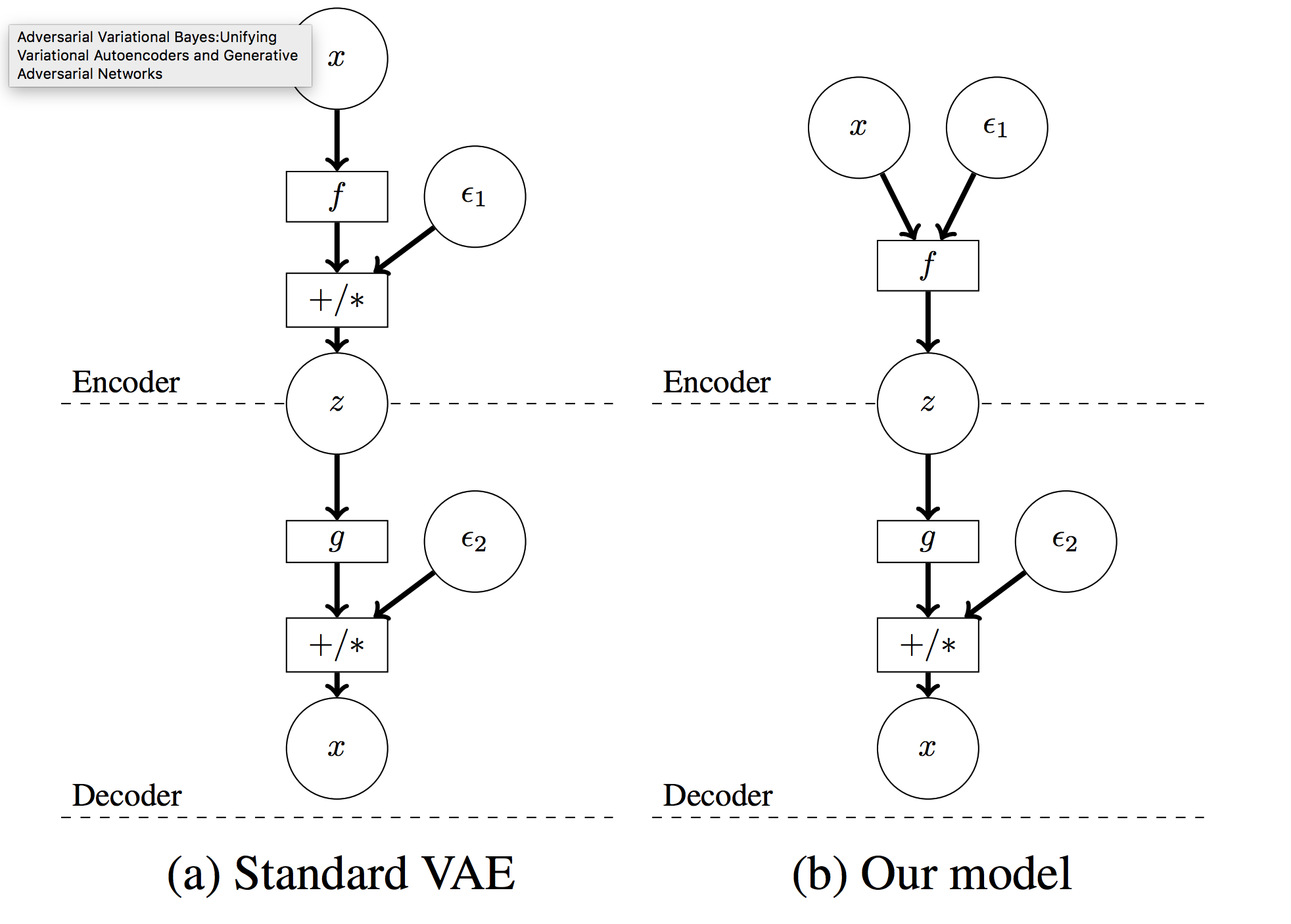Adversarial Variational Bayes apply gan loss to VAE framework. AVB is different from former VAE in 2 ways: x is inserted to the encoder with noise(epsilon) and the encoder output z. Also, instead of KL divergence, discriminator is used to keep z to the prior. The second difference seems similar to that of AAE, but key difference is that the discriminator distinguishes pairs of x and z from pairs of x and priors. Algorithm is as follows. Discriminator may not work well in the case when two densities are very differnt. This paper use a technique called “Adaptive Contrast” that provide auxiliary conditional probability distribution r and calculate the contrast between r and q. Therefore, variational lowerbound is
$E_{P_{mathcal{D}}}(x)[-KL(q_{\phi})(z|x, r_{\alpha}(z|x)) + E_{q_{\phi}(z|x)}(-logr_{\alpha}(z|x)+logp_{\phi}(x, z))]$
Models are trained to maximize
$E_{P_{mathcal{D}}}E_{q_{\phi}(z|x)}(-T^*(x,z) -logr_{\alpha}(z|x)+logp_{\phi}(x, z))$

So?

AVB was able to capture more complex posterior distribution and resulted in much better log liklihood and KL divergence in MNIST.

Critic

Interesting idea. Planned to implement with Pytorch soon.

Mescheder, Lars, Sebastian Nowozin, and Andreas Geiger. “Adversarial variational bayes: Unifying variational autoencoders and generative adversarial networks.” arXiv preprint arXiv:1701.04722 (2017).