WHY?

Former CNNs were not spatially invariant.

WHAT?

Spatial Transformer Module can make a former CNN model invariant to cropping, translation, scale, rotation and skew without greatly increasing the computation cost. ST module consists of 3 parts: localisation network, grid generator, and sampler. 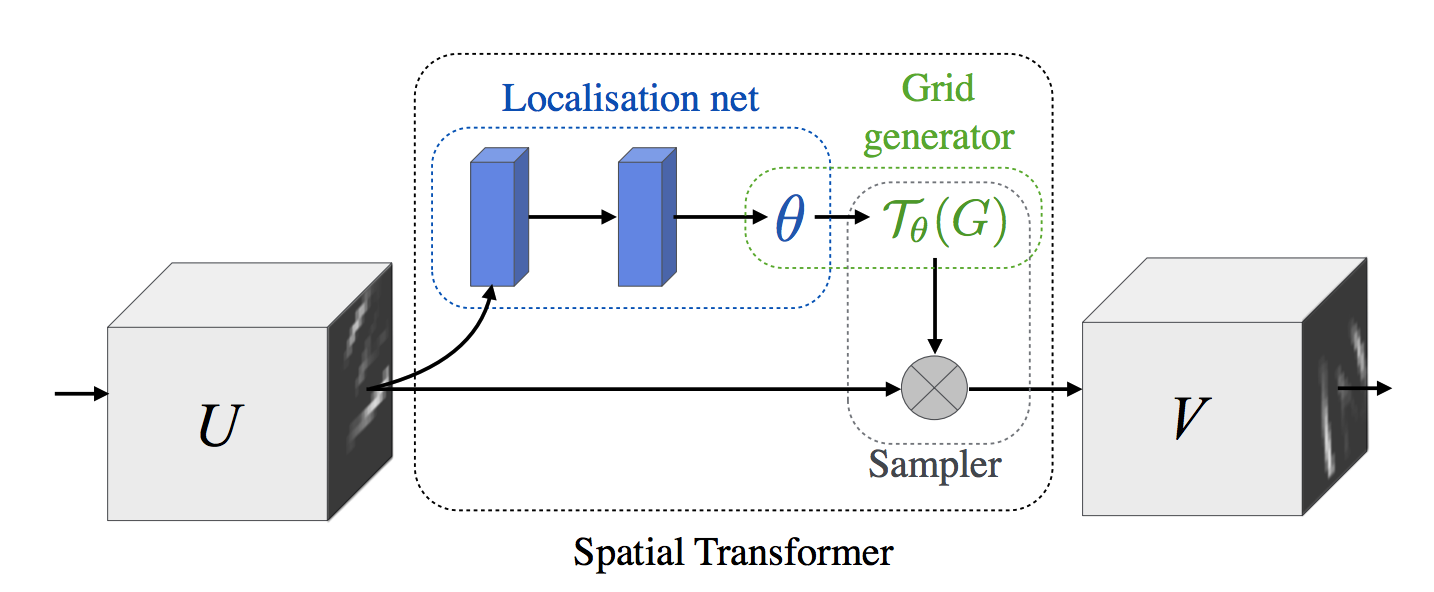Localisation network takes input feature map ($U \in \mathbb{R}^{H X W X C}$ and output $\theta$ the parameter of the transformation $\tau_{\theta}$. Next, grid generator transform the coordinate of target pixel into the corresponding coordinate of source pixel. This is like designating the location of input pixels in the space of output feature map. For example, affine transformation need six parameter. Lastly, the sampler is used to get the value of each pixel of output feature map. Sampling kernel uses the resulted coordinate of source pixel to get the output value. Backpropagation is possible since we can calculate the partial derivative of sampling kernel. $\theta = f_{loc}(U)\\ \left( \begin{array}{c} x_i^s \\ y_i^s \end{array} \right) = \tau_{\theta}(G_i) = A_{\theta} \left( \begin{array}{c} x_i^t \\ y_i^t \\ 1 \end{array} \right) = \left[ \begin{array}{ccc} \theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21} & \theta_{22} & \theta_{23} \end{array} \right] \left( \begin{array}{c} x_i^t \\ y_i^t \\ 1 \end{array} \right)\\ V_i^c = \Sigma_n^H \Sigma_m^W U^c_{nm} k(x_i^s - m; \Phi_x)k(y_i^s - m; \Phi_y)$ Multile spatial transformer can be used in a single CNN model to detect multiple objects.

So?

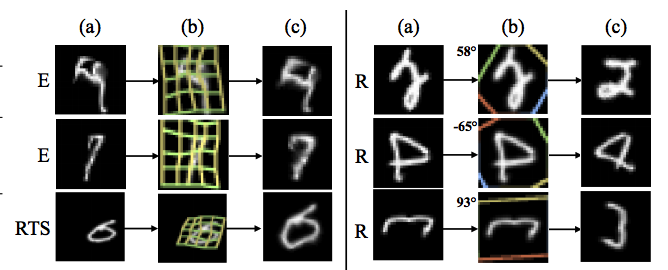ST-CNN achieved state of the art performance on Distorted MNIST, SVHN and fine-grained fine classification.

Critic

Since I am not familiar with traditional graphics and vision, the idea of mapping seems surprising. I wonder this idea can be applied to 3d object detection.

Jaderberg, Max, Karen Simonyan, and Andrew Zisserman. “Spatial transformer networks.” Advances in neural information processing systems. 2015.