Note

• Importance Sampling

WHY?

기존의 VAE는 posterior inference를 할때 posterior가 factorial하고 parameter들이 observations로 부터 non-linear regression 가능하다고 전제한다. 이러한 전제는 overly simplified되어 있어서 model capacity를 충분히 활용하지 못한다.

WHAT?

$log p(x) = log \mathbb{E}_{q(h|x)}[\frac{p(x,h)}{q(h|x)}] \geq \mathbb{E}_q(h|x)[log \frac{p(x,h)}{q(h|x)}] = \mathcal{L}(x)$
기존의 VAE는 위 식의 우항을 목적식으로 가진다. 하지만 IWAE(Importance Weighted Autoencoder)는 log p(x)를 추정하기 위하여 k-sample importance weighting estimate of log-likelihood를 사용한다. h는 recognition model에서 추출된 독립 샘플이다.
$\mathcal{L}_k(x) = \mathbb{E}_{h_1,...,h_k \sim q(h|x)}[log \frac{1}{k}\Sigma_{i=1}^k\frac{p(x,h_i)}{q(h_i|x)}]\\ w_i = p(x, h_i)/q(h_i|x)\\ \mathcal{L}_k = \mathbb{E}[\frac{1}{k}\Sigma_{i=1}^k w_i] = log p(x)$ 학습을 위한 gradient는 아래와 같이 구한다. 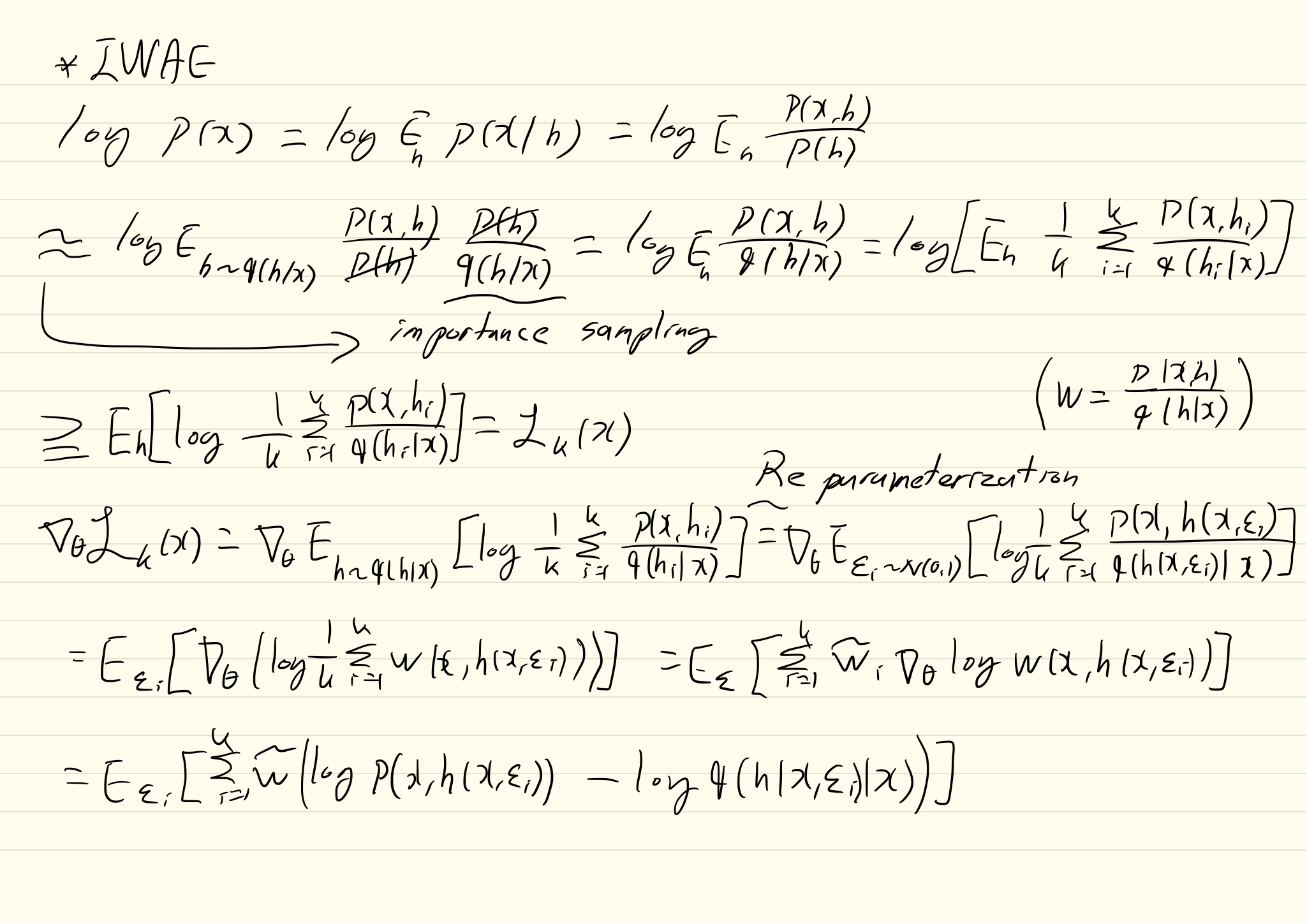마지막 항의 gradient를 평균내서 구한다. 보통 mini batch내에서 평균을 내며 k가 커질 수록 lowerbound가 커진다는 것이 증명되어 있다.

So?

MNIST와 OMNIGLOT 데이터에 대하여 좋은 NLL을 보였다. 특히 여러층의 VAE에서 hidden unit들이 죽는 현상을 어느 정도 해결하였다.

Critic

수학 공부를 하자

Burda, Yuri, Roger Grosse, and Ruslan Salakhutdinov. “Importance weighted autoencoders.” arXiv preprint arXiv:1509.00519 (2015).