WHY?

VAE는 generation에 상당히 강력한 도구이지만 conditional stochastic variable을 통하여 생성하기 때문에 계층적인 특징을 학습하는 깊은 모델을 만들기 어렵다.

WHAT?

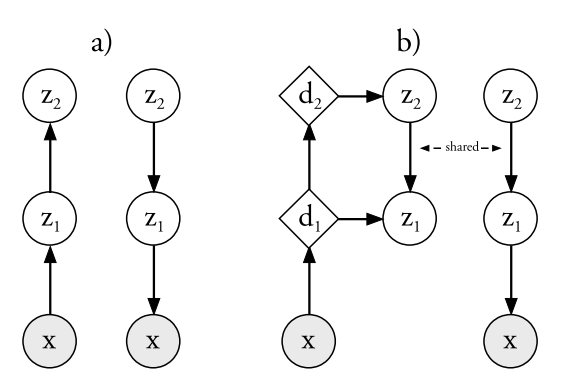기존의 VAE와 LVAE의 generative model은 같다. $p_{\theta}(z) = p_{\theta(z_L)}\Pi_{i=1}^{L-1}p_{\theta}(z_i|z_{i+1})\\ p_{\theta}(z_i|z_{i+1}) = N(z_i|\mu_{p,i}(z_{i+1}), \sigma^2_{p,i}(z_{i+1})), p_{\theta}(z_L) = N(z_L|0, I)\\ p_{\theta}(x|z_1) = N(x|\mu_{p,0}(z_{1}), \sigma^2_{p,0}(z_{1})) or P_{\theta}(x|z_1)=B(x|\mu_{p,0}(z_1))$ 기존의 VAE를 계층적으로 만들 경우, inference model과 generative model 사이에는 아무런 연관성이 없다. Ladder-VAE는 inference model은 generative model의 parameter를 precision-weighted combination하여 활용한다.
$q_{\phi}(z|x) = q_{\phi}(z_L|x)\Pi_{i=1}^{L-1}q_{\phi}(z_i|z_{i+1})\\ \sigma_{q,i} = \frac{1}{\hat{\sigma_{q, i}}^{-2} + \sigma_{p, i}^{-2}}\\ \mu_{q,i} = \frac{\hat{\mu}_{q,i}\hat{\sigma_{q, i}}^{-2} + \mu_{p,i}\sigma_{p, i}^{-2}}{\hat{\sigma_{q, i}}^{-2} + \hat{\sigma_{p, i}}^{-2}}\\ q_{\phi}(z_i|\cdot)=N(z_i|\mu_{q,i}, \sigma^2_{q,i})$

So?

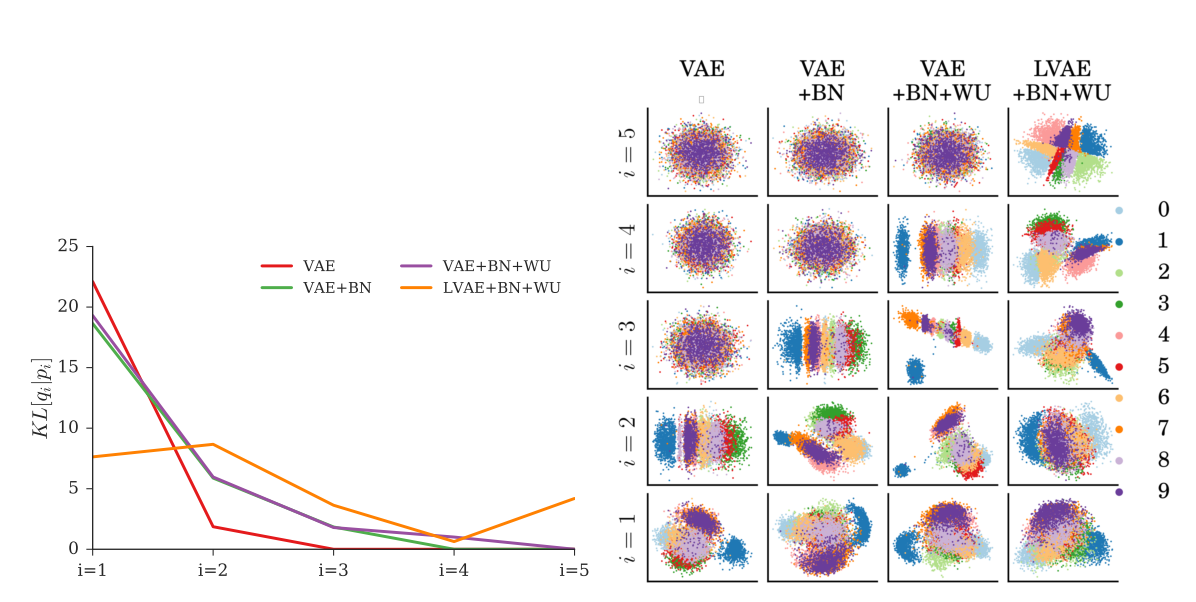MNIST, OMINGLOT, NORB데이터들에 대하여 높은 log-liklihood score를 얻었을 뿐 만 아니라 여러 층의 latent variable들이 의미를 골고루 포함하고 있는 것을 볼 수 있다.

Critic

각 층의 latent variable들을 잘 활용하고 있기는 하지만 각 층의 latent variable들이 semantic한 의미의 hierarchical feature를 학습한 것 같지는 않아 아쉽다.

Sønderby, Casper Kaae, et al. “Ladder variational autoencoders.” Advances in neural information processing systems. 2016.