Note

Information bottleneck이론이란 데이터 X로부터 관련 정보인 Y로 정보를 압축할 때 Y와의 관련성(accuracy)과 X의 압축성(compression)사이의 최고의 tradeoff를 정보량을 통하여 찾는 기법을 말한다. $R_{IB}(\theta) = I(Z, Y; \theta) - \beta I(Z, X; \theta)$

WHY?

Deep learning model의 성능을 Information bottleneck을 통하여 최적화 하려는 시도는 있었지만 IB의 목적식을 variational inference를 통하여 추정하려는 시도는 이루어지지 않았다.

WHAT?

위에서 주어진 IB의 목적식은 joint probability로 나타낼 수 있다. 하지만 그 중의 일부는 직접적으로 구할 수 없기 때문에 q를 통하여 variational inference를 한다. 그 결과 위 IB식의 lower bound는 다음과 같이 나온다. $I(Z, Y; \theta) - \beta I(Z, X; \theta) \\ \int dx dy dz p(x) p(y|x) p(z|x) log q(y|z)\\ -\beta \int dx dz p(x) p(z|x) log \frac{p(z|x)}{r(z)} = L$ 실제로 이 식을 구하기 위해서 Monte Carlo기법과 reparameterization trick을 사용한다. p(x, y)는 sampling할 수 있기 때문에 $L \approx \frac{1}{N}\Sigma_{n=1}^{N}[\int dz p(z|x_n)log q(y_n|z) - \beta p(z|x_n)log \frac{p(z|x_n)}{r(z)}]$ 로 나타낼 수 있다. 또한 인코더 형식의 p(z|x)를 vae에서 사용하는 인코더 처럼 사용하여 $\mu$와 $\sigma$를 뽑아서 reparameterization trick을 사용한다면 back prop을 할 수 있다. r(z)를 쉬운 prior, 예를 들어 gaussian으로 놓는다면 p(z|x)와 r(z)의 KLD를 analytic하게 구할 수 있어 최종 목적식은 다음과 같이 된다. $J_{IB} = \frac{1}{N}\Sigma^{N}_{n=1} E_{\epsilon \sim p(\epsilon)} [-log q(y_n|f(x_n, \epsilon))] + \beta KL[p(z|x_n), r(Z)]$ 이는 beta-VAE의 목적식에서 reconstruction loss를 classification loss로 바꾼 것과 같다.

So?

이 모델로 classifier를 학습할 경우 적당한 숫자의 $\beta$를 주는 것 만으로 왠만한 regularization(dropout/cp)이 주는 성능 향상을 얻을 수 있다. 이 모델에서 $\beta$의 값을 변화하며 여러 현상을 관찰 할 수 있는데 가장 인상적이었던 부분은 regularization이었다. 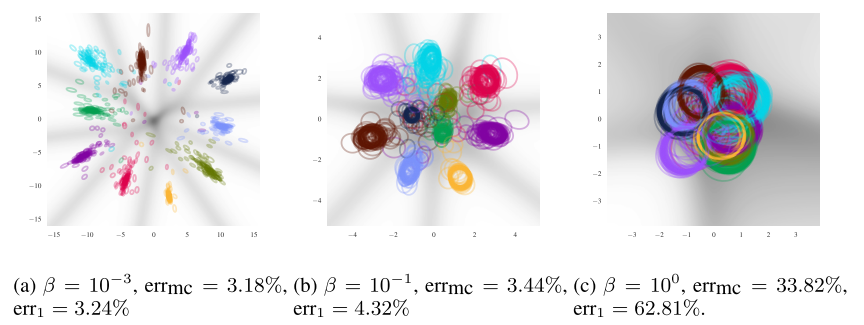작은 $\beta$값의 의미는 X와 Z의 정보를 크게 줄이지 않겠다는 것이다. 그리하여 overfit이 일어나고 Y에만 집중하여 우리가 가정한 prior에 크게 벗어나게 된다. 너무 큰 $\beta$값은 우리가 제시한 prior에 너무 모이게 되어 모델의 성능을 저하한다. 하지만 적당한 값의 $\beta$는 각 class별로 적당한 분포를 만들어 모인다. 이를 보면 알 수 있듯이 좋은 $\beta$를 사용하면 Adversarial attck에 크게 robust해진다.

Critic

Deep learning모델을 정보이론 관점에서 설명하여 색다르고 모델에 대하여 깊이 이해할 수 있게 된 것 같다. 반면 모델의 실질적인 성능을 향상시키는데 이용되지 못한 것이 아쉽다.

Alemi, Alexander A., et al. “Deep variational information bottleneck.” arXiv preprint arXiv:1612.00410 (2016).