WHY?

기존의 autoencoder는 이미지나 음성과 같은 연속형 데이터에 대한 latent structure를 잘 잡았지만 텍스트와 같은 discrete한 데이터의 latent structure를 잡는 것은 어려웠다.

WHAT?

Adversarially regularized autoencoder는 discrete한 데이터들을 latent space에 smooth하게 plot하는 것이 목적이다. 이를 위하여 특정 분포(Gaussian Normal)을 가정하고 latent의 분포를 이에 Wasserstein distance를 이용하여 근사시키는 방법을 사용한다. 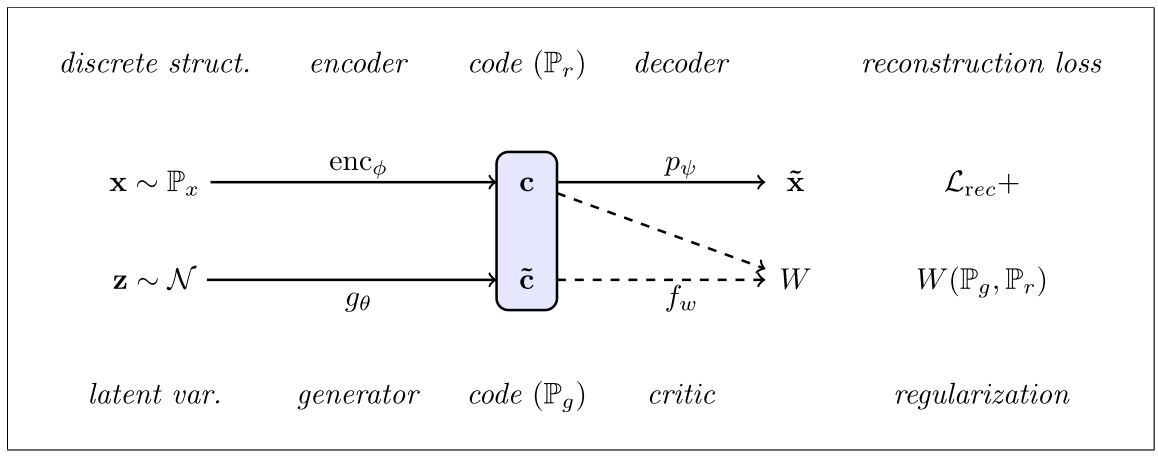목적식은 다음과 같다. $min_{\phi, \psi, \theta} L_{rec}(\phi, \psi) + \lambda^{(1)}W(P_r, P_g)$ 이를 세부적으로 풀면 세가지 항으로 나눌 수 있다. $1) min_{\phi, \psi, \theta} L_{rec}(\phi, \psi)\\ 2)min_{w \in W} L_{cri}(w) = max_{w \in W} E_{x \sim p_x}[f_w(enc_{\phi}(x))] - E_{\bar{c} \sim P_g}[f_w(\tilde{c})]\\ 3)min_{\phi, \psi} L_{encs}(\phi, \psi) = min_{\phi, \psi, \theta} E_{x \sim p_x}[f_w(enc_{\phi}(x))] - E_{\bar{c} \sim P_g}[f_w(\tilde{c})]$ 학습은 세 단계로 이루어 지는데 우선 reconstruction을 위하여 autoencoder를 학습시키고 generator와 encoder의 결과물 사이의 Wasserstein distance를 계산하는 critic을 학습하고 마지막으로 encoder와 generator를 critic에 대하여 adversarial하게 학습한다. 알고리즘은 다음과 같다. 이 과정에서 데이터가 가지고 있는 추가적인 알려진 성질(ex-sentiment)를 conditional하게 제공하고 이를 구분하는 classifier를 추가적으로 학습시킴으로서 code space transfer도 가능하다.

So?

이를 통하여 discrete한 text데이터들로 부터 continuous하면서도 meaningful한 latent variable을 얻는데 성공하였다.

Critic

discrete한 데이터를 continous하게 represent했다는 점에서 의의가 있지만 논문에서 제시한 qualitative한 성과를 가지고 latent variable들이 meaningful하다고 판단할 수 있는지 의문이다. 무엇보다 fluent한 reconstruction이 제한적이어서 다소 아쉽다.

Kim, Yoon, et al. “Adversarially regularized autoencoders for generating discrete structures.” arXiv preprint arXiv:1706.04223 (2017).